A pendulum bob is swinging in a vertical plane such that its angular amplitude is less than 90∘. At its highest point, the string is cut. Which trajectory is possible for the bob afterwards ?

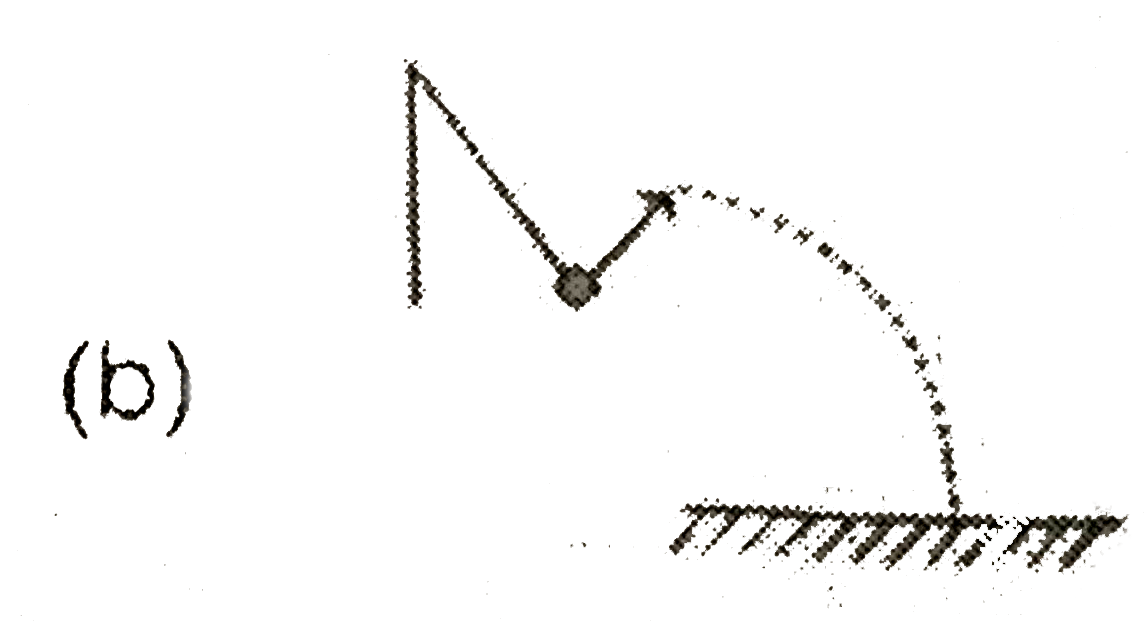
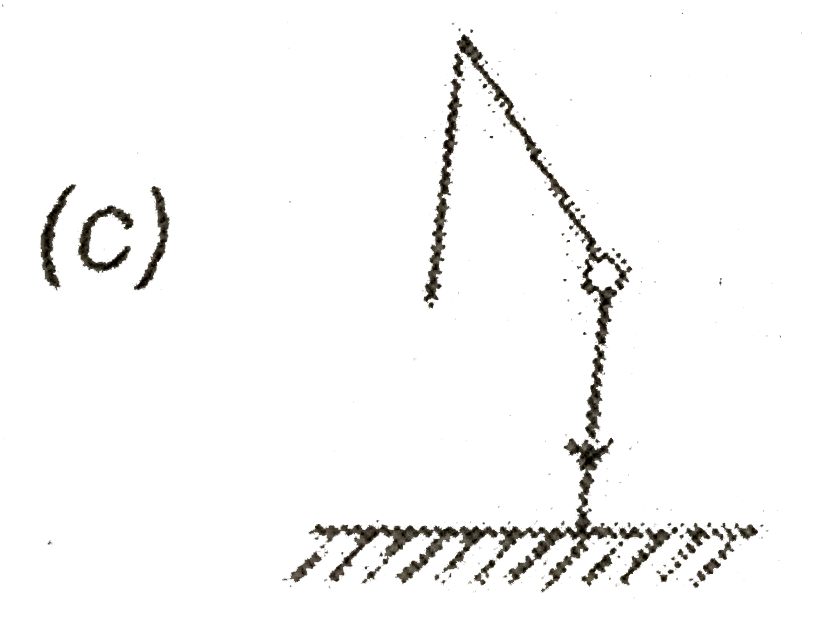

The correct Answer is:C
To solve the problem, we need to analyze the motion of the pendulum bob at the moment the string is cut. Here’s the step-by-step solution:
Step 1: Understand the Initial Conditions
The pendulum bob is swinging in a vertical plane with an angular amplitude of less than 90 degrees. At its highest point in the swing, the bob momentarily comes to rest before the string is cut.
Hint: Remember that at the highest point of a pendulum swing, the velocity is zero.
Step 2: Analyze Forces Acting on the Bob
When the string is intact, the forces acting on the bob include the tension in the string and the gravitational force (weight) acting downwards. At the highest point, the tension is at its minimum, but it is still present.
Hint: Consider what happens to the forces when the string is cut.
Step 3: Effect of Cutting the String
Once the string is cut, the tension in the string becomes zero. The only force acting on the bob is its weight (mg), which acts downward.
Hint: Think about Newton's second law and how the absence of tension affects the motion of the bob.
Step 4: Determine the Motion of the Bob
Since the only force acting on the bob after the string is cut is the gravitational force (mg), the bob will experience an acceleration equal to g (acceleration due to gravity) directed downward.
Hint: Remember that the direction of acceleration determines the direction of motion.
Step 5: Conclude the Trajectory
At the moment the string is cut, the bob has zero velocity (it is at the highest point). With only gravitational force acting on it, the bob will begin to fall straight down under the influence of gravity. Therefore, the trajectory of the bob after the string is cut will be a straight vertical line downward.
Hint: Visualize the motion of an object in free fall to understand the trajectory.
Final Answer
The possible trajectory for the bob after the string is cut is a straight downward path.
The pendulum bob is swinging in a vertical plane with an angular amplitude of less than 90 degrees. At its highest point in the swing, the bob momentarily comes to rest before the string is cut.
When the string is intact, the forces acting on the bob include the tension in the string and the gravitational force (weight) acting downwards. At the highest point, the tension is at its minimum, but it is still present.
Once the string is cut, the tension in the string becomes zero. The only force acting on the bob is its weight (mg), which acts downward.
Since the only force acting on the bob after the string is cut is the gravitational force (mg), the bob will experience an acceleration equal to g (acceleration due to gravity) directed downward.
At the moment the string is cut, the bob has zero velocity (it is at the highest point). With only gravitational force acting on it, the bob will begin to fall straight down under the influence of gravity. Therefore, the trajectory of the bob after the string is cut will be a straight vertical line downward.
The possible trajectory for the bob after the string is cut is a straight downward path.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Advanced
24 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
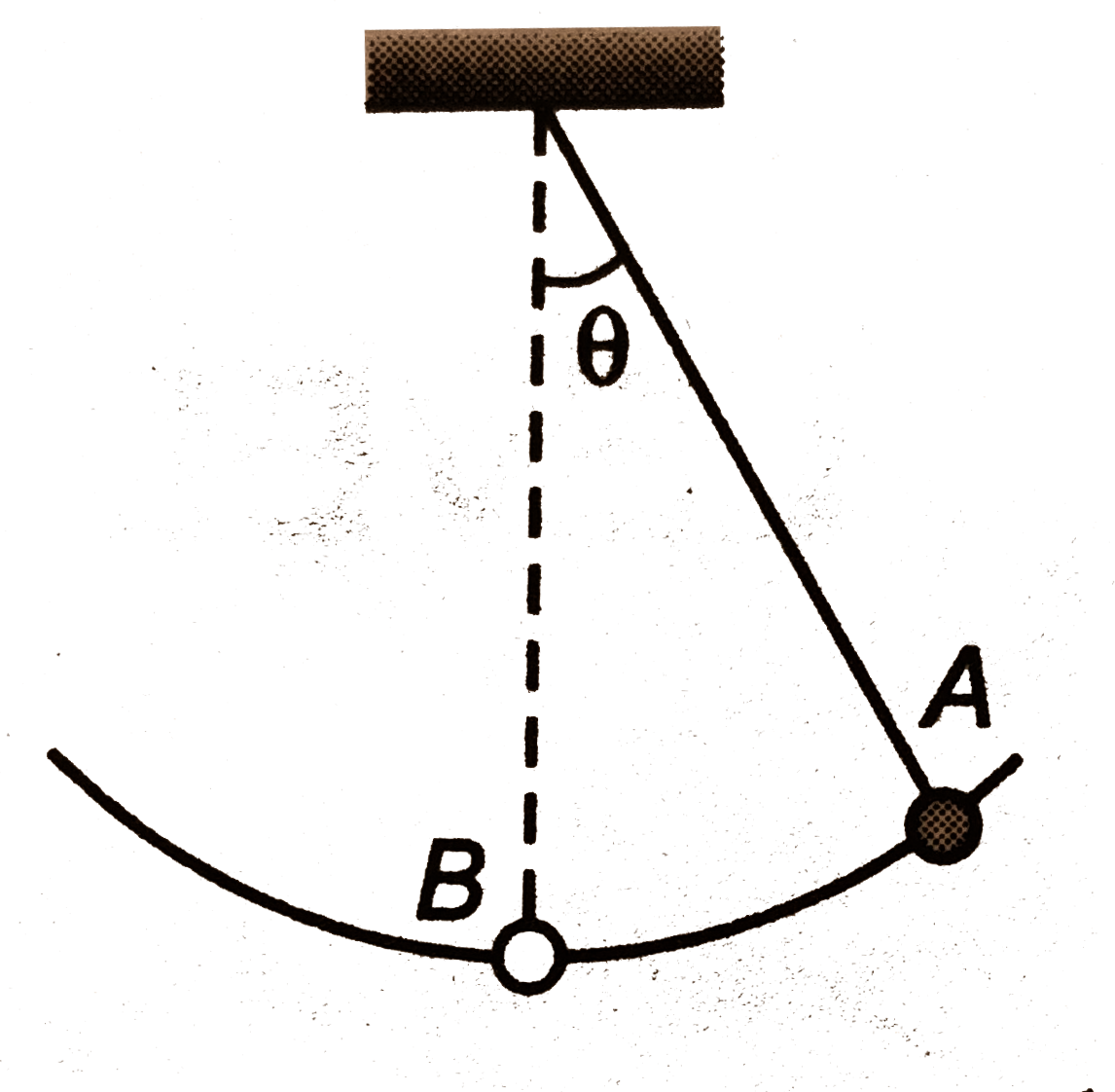
A ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionThe angular amplitude of a simple pendulum is θ0. The maximum tension in its string will be
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘ true
false
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
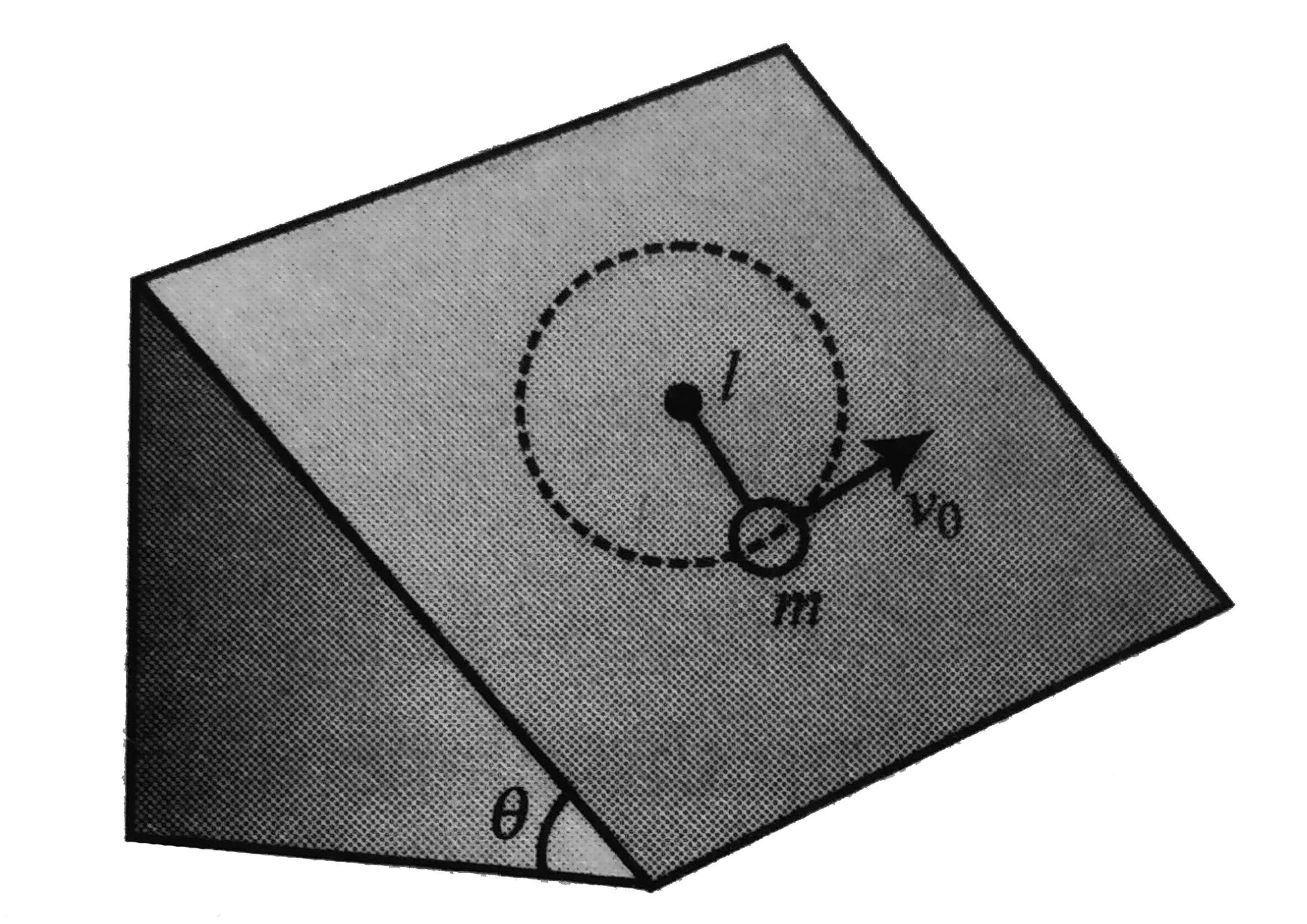
The speed of the bob at the highest point on the circle is
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
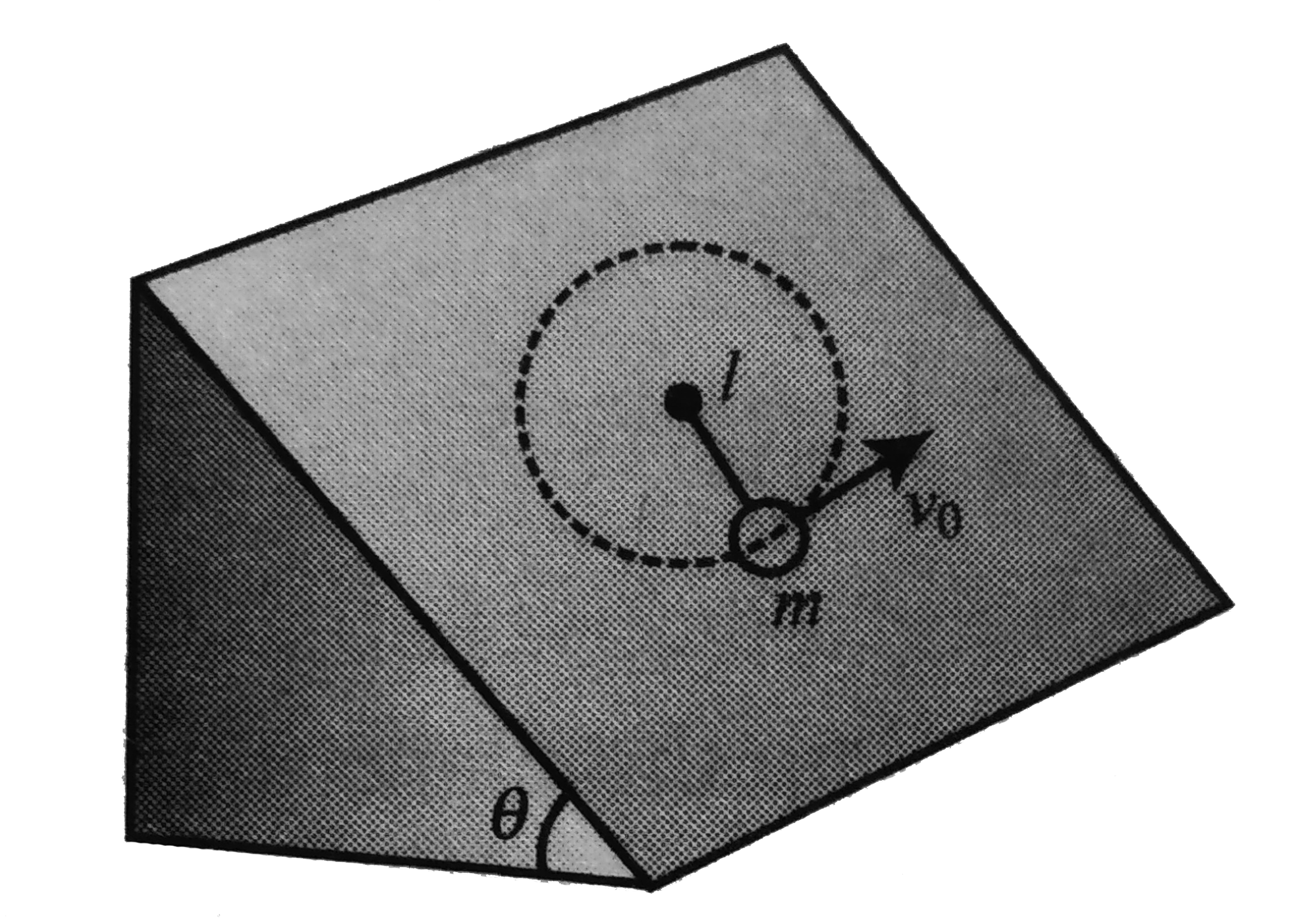
The speed of the bob at the lowest point is
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
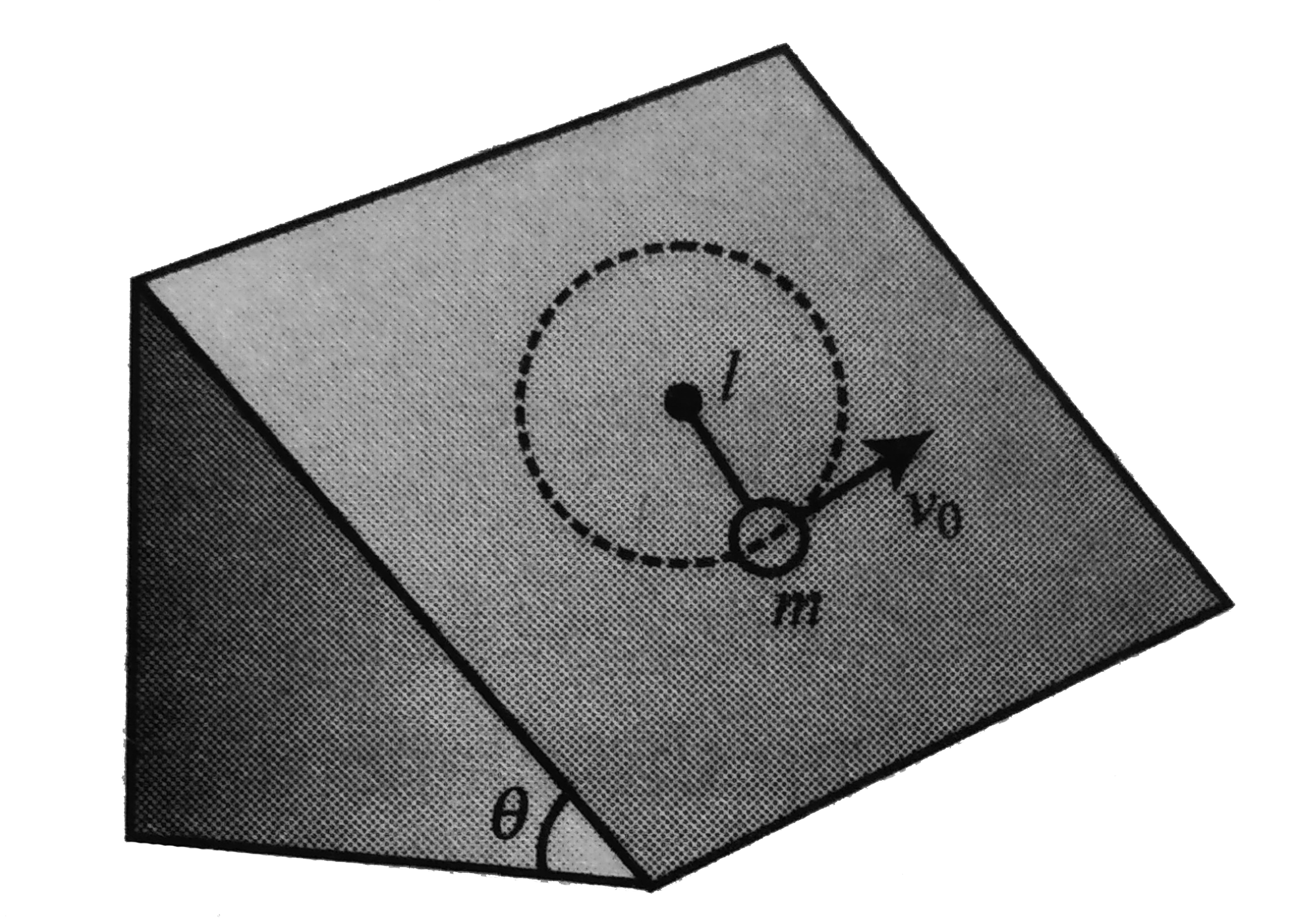
The tension in the string at the highest position is
View Solution
