A bucket water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmospheric pressure at the bottom is
0.5 kPa
1 kPa
5kPa
None of these
The correct Answer is:B
To solve the problem, we need to find the water pressure above atmospheric pressure at the bottom of a bucket filled with water. The bucket is tied to a rope that goes over a frictionless pulley, with a weight on the other end that is half the mass of the bucket plus water.
1. Identify the Variables:
- Let h=15cm=0.15m (height of water in the bucket).
- Let m be the mass of the bucket filled with water.
- The mass of the weight tied to the rope is m2.
2. Determine the Forces Acting on the Bucket:
- The forces acting on the bucket are:
- The gravitational force acting downwards: mg
- The tension in the rope acting upwards: T
- According to Newton's second law, for the bucket:
mg−T=ma
- Here, a is the acceleration of the bucket.
3. Determine the Forces Acting on the Weight:
- The forces acting on the weight are:
- The gravitational force acting downwards: m2g
- The tension in the rope acting upwards: T
- For the weight, we can write:
T−m2g=−m2a
4. Solve the Equations:
- From the first equation:
T=mg−ma
- From the second equation:
T=m2g−m2a
- Setting the two expressions for T equal:
mg−ma=m2g−m2a
- Simplifying this gives:
mg−m2g=ma−m2a
- Factoring out m:
12mg=12ma
- Thus, we find:
g=a
5. Find the Effective Gravitational Force:
- The effective gravitational force acting on the water in the bucket is:
geff=g−g3=2g3
6. Calculate the Pressure at the Bottom of the Bucket:
- The pressure at the bottom of the bucket is given by:
P=h⋅ρ⋅geff=h⋅ρ⋅2g3
- Substituting h=0.15m:
P=0.15⋅ρ⋅2g3
- Assuming ρ=1000kg/m3 (density of water) and g≈9.81m/s2:
P=0.15⋅1000⋅2⋅9.813=0.15⋅1000⋅6.54≈981Pa=0.981kPa
7. Final Result:
- The pressure above atmospheric pressure at the bottom of the bucket is approximately 1kPa.
- Let h=15cm=0.15m (height of water in the bucket).
- Let m be the mass of the bucket filled with water.
- The mass of the weight tied to the rope is m2.
- The forces acting on the bucket are:
- The gravitational force acting downwards: mg
- The tension in the rope acting upwards: T
- According to Newton's second law, for the bucket:
mg−T=ma
- Here, a is the acceleration of the bucket.
- The forces acting on the weight are:
- The gravitational force acting downwards: m2g
- The tension in the rope acting upwards: T
- For the weight, we can write:
T−m2g=−m2a
- From the first equation:
T=mg−ma
- From the second equation:
T=m2g−m2a
- Setting the two expressions for T equal:
mg−ma=m2g−m2a
- Simplifying this gives:
mg−m2g=ma−m2a
- Factoring out m:
12mg=12ma
- Thus, we find:
g=a
- The effective gravitational force acting on the water in the bucket is:
geff=g−g3=2g3
- The pressure at the bottom of the bucket is given by:
P=h⋅ρ⋅geff=h⋅ρ⋅2g3
- Substituting h=0.15m:
P=0.15⋅ρ⋅2g3
- Assuming ρ=1000kg/m3 (density of water) and g≈9.81m/s2:
P=0.15⋅1000⋅2⋅9.813=0.15⋅1000⋅6.54≈981Pa=0.981kPa
- The pressure above atmospheric pressure at the bottom of the bucket is approximately 1kPa.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope when the cat move upwards with in acceleration a=2m/s2 relative to the rope ?

View SolutionA person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View SolutionA man pulls a bucket of water from a depth of h from a well. If the mass of the rope and that of bucket full of water are m and M respectively, the work done by the man is :
View SolutionA mam of mass 50 g stands on a frame of mass 30 g. He pulls on a light rope which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium what force man must exert on the rope?
View SolutionA bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm respectively. Find the height of the bucket.
View SolutionAs shown in figure a monkey of 20g mass is holding a light rope that passes over a frictionless pulley. A bunch of bananas of the same mass is tied to the other end of rope. Inorder to get access to the bunch the monkey starts climbing the rope. The distance between the monkey and the bananas is

View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View SolutionTwo bodies of masses m1 and m2(m1>m2) respectively are tied to the ends j of a string which passes over a light frictionless pulley. The masses are intitially at rest and released. What is the acceleration of the centre of mass ?
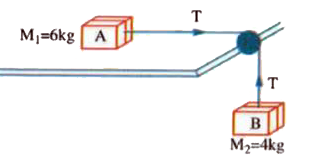
View SolutionA block A of mass 6kg is applied on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 4kg at the other end. Find the acceleration of the system and tension in the thread (given g=10ms−2)
View Solution
