A tube of small uniform cross section is used to siphon the water from the vessel. Then choose the correct alternative (s) :
(ρwater=103kg/m3,g=10m/s2,Patm=105Pa)

Water will come out from section B with a velocity of √80m/s
The greatest value of h1 for which the siphon will work is 10 m.
both are correct
both are wrong
The correct Answer is:A
Step by step video & image solution for A tube of small uniform cross section is used to siphon the water from the vessel. Then choose the correct alternative (s) : (rho_("water") = 10^(3) kg//m^(3), g = 10 m//s^(2), P_(atm) = 10^(5) Pa) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
An air filled balloon is at a depth of 1km below the water level in an ocean . The normal stress of the balloon (in Pa) is
(Given,ρwater=103kgm−3,g=9.8ms−2 and Patm=105Pa)
View SolutionA tank of large base area is filled with water up to a height of 5m. A hole of 2cm2 cross section in the bottom allows the water to drain out in continuous streams. For this situation, mark out the correct statement(s) (take ρwater=1000kg/m3,g=10ms−12)

View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
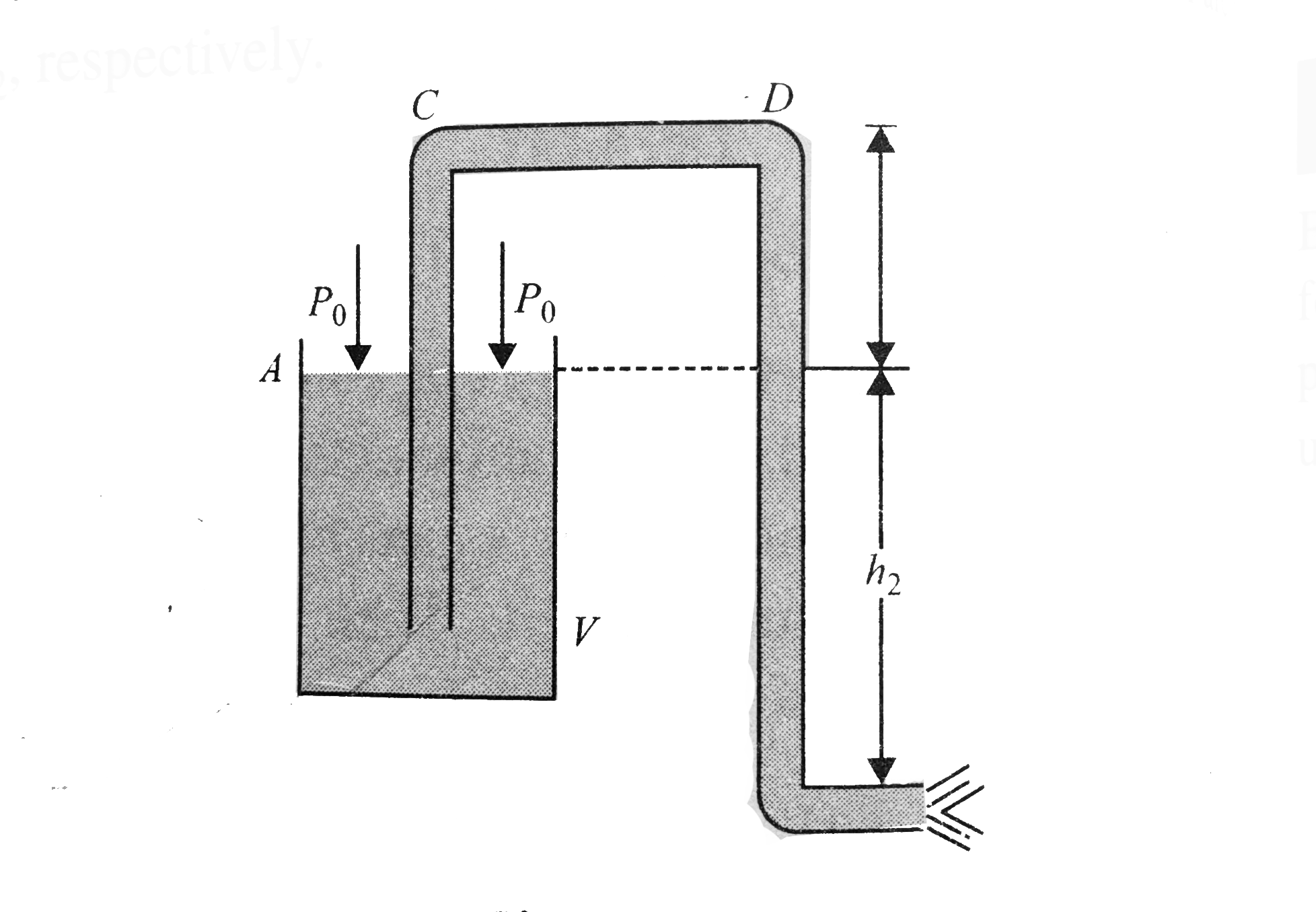
If h1=h2=3.0m, the maximum value of h1, for which the siphon will work will be
View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
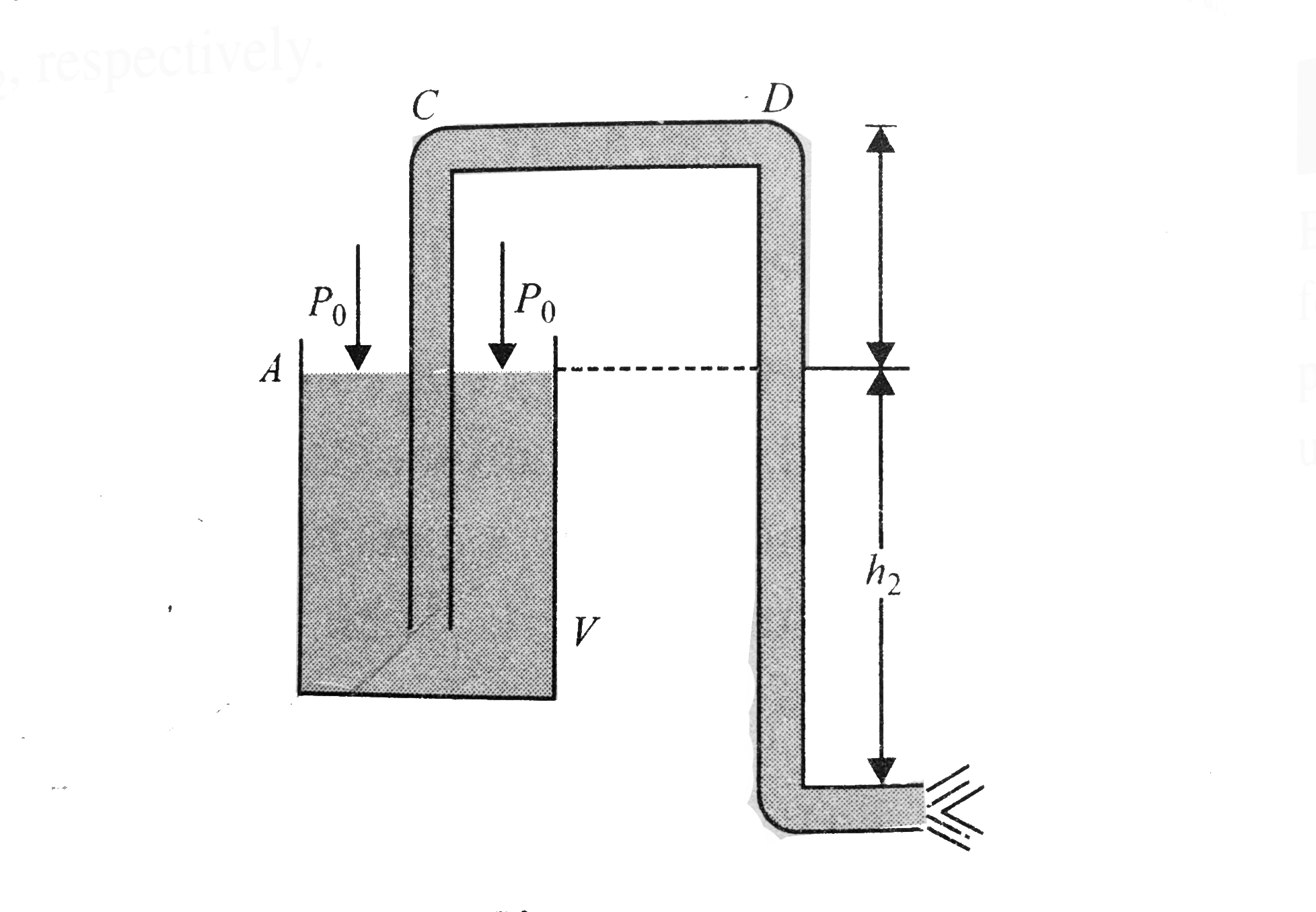
Given h1=h2=3.0m, the gauge pressure of water in the highest level CD of the tube will be
View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.

Determine the velocity vB of the water issuing out at B.
View SolutionThe guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View SolutionIn a carburator of an engine, aire is drawn from atmosphere through section A with a velocity of 10m/s. The narrow section B is connected to a petrol tank as shown. The minimum ratio of area of cross section A to area of cross section B, so that the petrol can just enter the carburator tube is √66x. Then the value of x is : (density of petrol =1000kg/m3, density of air =2kg/m3,g=10m/s2 atmospheric pressure =105 Pa and assume density of air remain constant)

View SolutionA metallic sphere of radius 1.0×10−3m and density 1.0×104kg/m3 enters a tank of water, after a free fall through a distance of h in the earth's gravitational field. If its velocity remains unchanged after entering water, determine the value of h. Given: coefficient of viscosity of water =1.0×10−3Ns/m2,g=10ms−12 and density of water =1.0×103kg/m3.
View Solution
