Two metal rods X and Y having equal cross-sectional areas are joined in series. One end of which is heated. After some time, the temperature gradient along each rod is foound to be uniform, but greater in X than that in Y. Which of the following can be inferred
both the rods may be of different lengths
The heat current is the same in both the rods
Both the rods are of equal lengths
X is better conductor of heat than Y
The correct Answer is:A, B
Step by step video & image solution for Two metal rods X and Y having equal cross-sectional areas are joined in series. One end of which is heated. After some time, the temperature gradient along each rod is foound to be uniform, but greater in X than that in Y. Which of the following can be inferred by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Two rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View Solution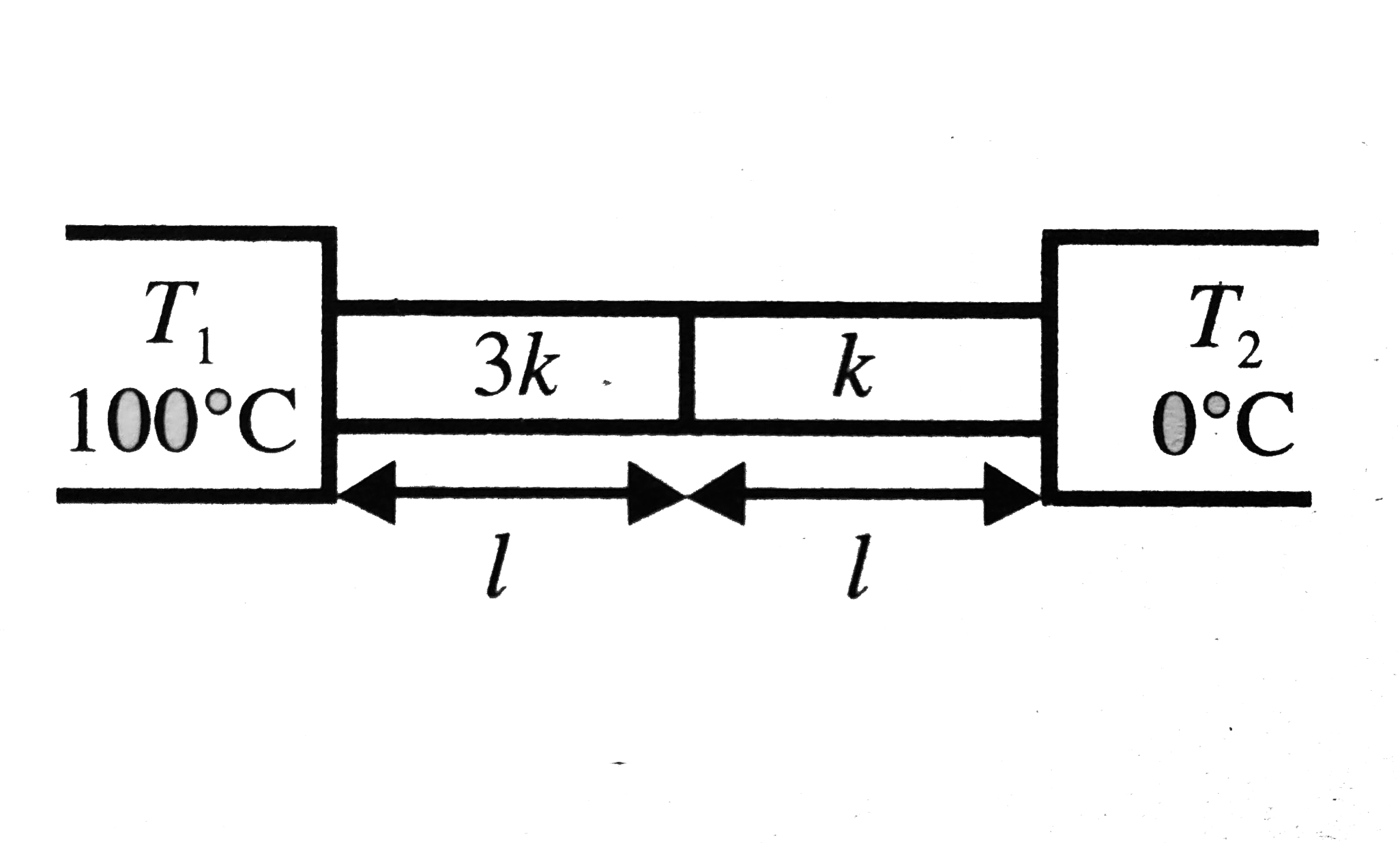
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.View Solution
Knowledge Check
- Question 1 - Select One
If x/y is a fraction greater than 1, then which one of the following must be less than 1?
A3y/xBx/3yC√xyDy/x
Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 View Solution
View SolutionA metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB=0.40J∘C−1 , thermal conductivity of the material of the rod. K=200Wm−1C−1 . Neglect any loss of heat to the atmosphere.
View SolutionA rod is made of uniform material and has non-uniform cross section. It is fixed at both the ends as shown and heated at mid-section. Which of the following are not correct?
 View Solution
View SolutionTwo identical rods of length (L), area of cross-sectional (A) and thermal conductivity k are joined end to end. If temperature difference of free ends is ΔT, the heat Q0 flows along rods per second. Find the total heat flowing per second along the rods if the two rods are placed parallel and temperature difference of free ends is ΔT. There is no heat loss from curved surface.
View SolutionA metal rod of length l, cross-sectional area A, Young's modulus Y and coefficient of linear expansion α is heated to t∘C. The work that can be performed by the rod when heated is
View SolutionTwo cylindrical rods of same cross-section area and same length are connected in series to an ideal cell as shown.The resistivity of left rod is ρ and that if right rod is 2ρ Then the variation of potential and electric field at any point P distant x from left end of combined rod system are given by
View SolutionTwo steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
View Solution

