A particle takes a time t1 to move down a straight tunnel from the surface of earth to its centre. If gravity were to remain constant this time would be t2 calculate the ratio t1t2
π2√2
π√2
√2π
π√2
The correct Answer is:A
To solve the problem, we need to calculate the time taken by a particle to move from the surface of the Earth to its center through a straight tunnel (denoted as t1) and compare it to the time taken if gravity were to remain constant (denoted as t2).
1. Understanding the Motion in the Tunnel:
- When a particle moves towards the center of the Earth, the gravitational force acting on it changes with distance. The force is maximum at the surface and decreases linearly to zero at the center.
- The gravitational acceleration g′ at a distance r from the center is given by:
g′=GM(r)r2
where M(r) is the mass enclosed within radius r.
2. Using the Concept of Simple Harmonic Motion (SHM):
- The motion of the particle can be modeled as simple harmonic motion. The time period T for one complete oscillation is given by:
T=2π√Rg
- However, since we are only interested in the time taken to reach the center, we take a quarter of the period:
t1=T4=14×2π√Rg=π2√Rg
3. Calculating t2 with Constant Gravity:
- If gravity were to remain constant throughout the tunnel, the particle would experience a constant acceleration g. The distance to the center of the Earth is R.
- Using the equation of motion s=ut+12at2 with initial velocity u=0, we have:
R=12gt22
- Rearranging gives:
t22=2Rg⟹t2=√2Rg
4. Finding the Ratio t1t2:
- Now we can find the ratio of t1 to t2:
t1t2=π2√Rg√2Rg
- Simplifying this expression:
t1t2=π2√2=π2√2
Final Result:
Thus, the ratio t1t2 is:
t1t2=π2√2
- When a particle moves towards the center of the Earth, the gravitational force acting on it changes with distance. The force is maximum at the surface and decreases linearly to zero at the center.
- The gravitational acceleration g′ at a distance r from the center is given by:
g′=GM(r)r2
where M(r) is the mass enclosed within radius r.
- The motion of the particle can be modeled as simple harmonic motion. The time period T for one complete oscillation is given by:
T=2π√Rg
- However, since we are only interested in the time taken to reach the center, we take a quarter of the period:
t1=T4=14×2π√Rg=π2√Rg
- If gravity were to remain constant throughout the tunnel, the particle would experience a constant acceleration g. The distance to the center of the Earth is R.
- Using the equation of motion s=ut+12at2 with initial velocity u=0, we have:
R=12gt22
- Rearranging gives:
t22=2Rg⟹t2=√2Rg
- Now we can find the ratio of t1 to t2:
t1t2=π2√Rg√2Rg
- Simplifying this expression:
t1t2=π2√2=π2√2
Thus, the ratio t1t2 is:
t1t2=π2√2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises31videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.620videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
A particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionA partical in SHM ha a period of 4s .It takes time t1 to start from mean position and reach half the amplitude. In another case it taken a time t2 to start from extreme position and reach half the amplitude. Find the ratio t1/t2
View SolutionA train accelerates from rest at a constant rate a for time t1and then it retards at the constant rate b for time t2 then comes to rest. Find the ratio t1/t2.
View Solution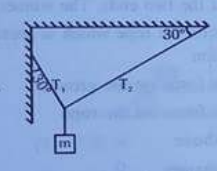
Calculate T1&T2.View SolutionA ring takes time t1 in slipping down an inclined plane of length L, whereas it takes time t2 in rolling down the same plane. The ratio of t1andt2 is -
View SolutionA point mives in a straight line so its displacement x mertre at time t second is given by x2=1+t2. Its aceleration in ms−2 at time t second is .
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?View SolutionA particle moves in a straight line and its position x at time t is given by x2=2+t. Its acceleration is given by :-
View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum
View Solution

