The charges on two spheres are +7μC and –5μC respectively. They experience a force F. If each of them is given an additional charge of –2μC, the new force of attraction will be
F
F/2
F/√3
2F
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Identify the initial charges and the force between them
The initial charges on the two spheres are:
- Charge on sphere 1, q1=+7μC=+7×10−6C
- Charge on sphere 2, q2=−5μC=−5×10−6C
The force F between them can be calculated using Coulomb's law:
F=k|q1⋅q2|r2
where k is Coulomb's constant, and r is the distance between the charges.
Step 2: Calculate the initial force
Substituting the values into the formula:
F=k|(+7×10−6)⋅(−5×10−6)|r2
This simplifies to:
F=k35×10−12r2
Step 3: Determine the new charges after adding the additional charge
Each sphere is given an additional charge of −2μC:
- New charge on sphere 1, q′1=+7μC−2μC=+5μC=+5×10−6C
- New charge on sphere 2, q′2=−5μC−2μC=−7μC=−7×10−6C
Step 4: Calculate the new force with the updated charges
Using Coulomb's law again for the new charges:
F′=k|q′1⋅q′2|r2
Substituting the new charges:
F′=k|(+5×10−6)⋅(−7×10−6)|r2
This simplifies to:
F′=k35×10−12r2
Step 5: Compare the new force with the initial force
Notice that:
F′=F
Thus, the new force of attraction remains the same as the initial force F.
Final Answer
The new force of attraction will be F.
---
The initial charges on the two spheres are:
- Charge on sphere 1, q1=+7μC=+7×10−6C
- Charge on sphere 2, q2=−5μC=−5×10−6C
F=k|q1⋅q2|r2
where k is Coulomb's constant, and r is the distance between the charges.
Substituting the values into the formula:
F=k|(+7×10−6)⋅(−5×10−6)|r2
This simplifies to:
F=k35×10−12r2
Each sphere is given an additional charge of −2μC:
- New charge on sphere 1, q′1=+7μC−2μC=+5μC=+5×10−6C
- New charge on sphere 2, q′2=−5μC−2μC=−7μC=−7×10−6C
Using Coulomb's law again for the new charges:
F′=k|q′1⋅q′2|r2
Substituting the new charges:
F′=k|(+5×10−6)⋅(−7×10−6)|r2
This simplifies to:
F′=k35×10−12r2
Notice that:
F′=F
Thus, the new force of attraction remains the same as the initial force F.
The new force of attraction will be F.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.310videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.410videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.110videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Two point charges +10 muC and +20 muC repel each other with a force of 100N. If a charge of-2 muC is added to each charge, then force between them will become
View SolutionTwo large parallel metal carry charges +Q and –Q respectively . A test charge q0 placed between them experiences a force F. If the separation between the plants is doubled, then the force on the test charge will be
View Solution
Knowledge Check
- Question 1 - Select One
Two point charges of +3μCand+4μC repel each other with a force of 10 N. If each is given an additional charge of −6μC, the new force is
A2 NB4 NC5 ND7.5 N
Two spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View SolutionTwo charges spheres are separated at a distance d exert a force F on each other, if charges are doubled and distance between them is doubled then the force is
View SolutionTwo charges of equal magnitudes and at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is
View SolutionIn the circuit given below, the charge in μC, on the capacitor having 5μF is
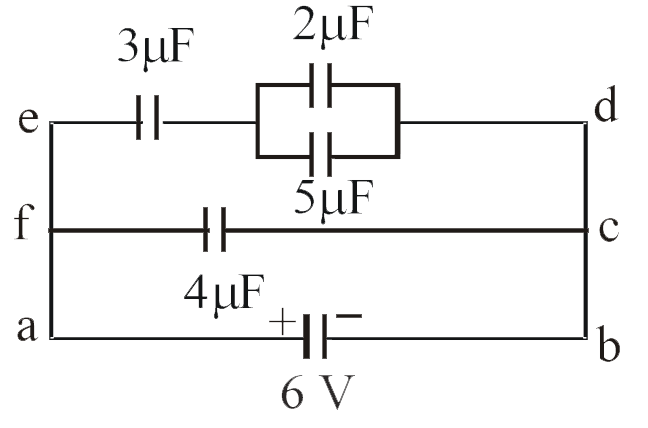 View Solution
View SolutionA solid conducting sphere of radius a is enclosed in a concentric shell of radius b>a. The charge on the inner sphere is 3μC and on the conducting shell is −10μC. The potential difference between the conductors is V. If +10μC additional charge is given to the outer shell, the new potential difference is
A. V
B. V/2
C. 2V
D. zeroView SolutionThe force of attractions between two charges 8μC and −4μC is 0.2 N. Find the distance of separation.
View SolutionTwo small conducting spheres of equal radius have charges +10μC and −20μC respectively and placed at a distance R from each other. They experience force F1. If they are brought in contact and separated to the same distance, they experience force F2. The ratio of F1 to F2 is
View Solution

