Fg and Fe represent gravitational and electrostatic force respectively between electrons situated at a distance 10 cm. The ratio of Fg/Fe is of the order of
1042
10−21
1024
10−43
The correct Answer is:D
To find the ratio of the gravitational force Fg to the electrostatic force Fe between two electrons situated at a distance of 10 cm, we can follow these steps:
Step 1: Write the formula for gravitational force
The gravitational force Fg between two masses is given by Newton's law of gravitation:
Fg=Gm1m2r2
For two electrons, m1=m2=me (mass of an electron), and the distance r=0.1m (10 cm converted to meters). Therefore:
Fg=Gm2er2
Step 2: Substitute the values for gravitational force
Using the universal gravitational constant G=6.67×10−11N m2/kg2 and the mass of an electron me=9.11×10−31kg:
Fg=(6.67×10−11)(9.11×10−31)2(0.1)2
Calculating (9.11×10−31)2:
(9.11×10−31)2=8.27×10−61
Now substituting this back:
Fg=(6.67×10−11)(8.27×10−61)0.01=5.52×10−710.01=5.52×10−69N
Step 3: Write the formula for electrostatic force
The electrostatic force Fe between two charges is given by Coulomb's law:
Fe=k|q1q2|r2
For two electrons, q1=q2=e (charge of an electron), and the distance r=0.1m:
Fe=ke2r2
Where k=9×109N m2/C2 and e=1.6×10−19C.
Step 4: Substitute the values for electrostatic force
Calculating e2:
e2=(1.6×10−19)2=2.56×10−38
Now substituting this back:
Fe=(9×109)(2.56×10−38)(0.1)2=(9×109)(2.56×10−38)0.01=2.304×10−26N
Step 5: Calculate the ratio FgFe
Now we can find the ratio:
FgFe=5.52×10−692.304×10−26
Calculating this gives:
FgFe=2.40×10−43
Conclusion
Thus, the ratio of the gravitational force to the electrostatic force between two electrons is:
FgFe≈2.4×10−43
The gravitational force Fg between two masses is given by Newton's law of gravitation:
Fg=Gm1m2r2
For two electrons, m1=m2=me (mass of an electron), and the distance r=0.1m (10 cm converted to meters). Therefore:
Fg=Gm2er2
Using the universal gravitational constant G=6.67×10−11N m2/kg2 and the mass of an electron me=9.11×10−31kg:
Fg=(6.67×10−11)(9.11×10−31)2(0.1)2
Calculating (9.11×10−31)2:
(9.11×10−31)2=8.27×10−61
Now substituting this back:
Fg=(6.67×10−11)(8.27×10−61)0.01=5.52×10−710.01=5.52×10−69N
The electrostatic force Fe between two charges is given by Coulomb's law:
Fe=k|q1q2|r2
For two electrons, q1=q2=e (charge of an electron), and the distance r=0.1m:
Fe=ke2r2
Where k=9×109N m2/C2 and e=1.6×10−19C.
Calculating e2:
e2=(1.6×10−19)2=2.56×10−38
Now substituting this back:
Fe=(9×109)(2.56×10−38)(0.1)2=(9×109)(2.56×10−38)0.01=2.304×10−26N
Now we can find the ratio:
FgFe=5.52×10−692.304×10−26
Calculating this gives:
FgFe=2.40×10−43
Thus, the ratio of the gravitational force to the electrostatic force between two electrons is:
FgFe≈2.4×10−43
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.3
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
If Fg,FN,FW and FE be the gravitational, nuclear, weak and electromagnetic forces respectively, then arrange them in proper order as per their strength.
View SolutionLet E,G and N represent the magnitudes of electromagnetic, gravitational and nuclear forces between two electrons at a given separation. Then
View Solution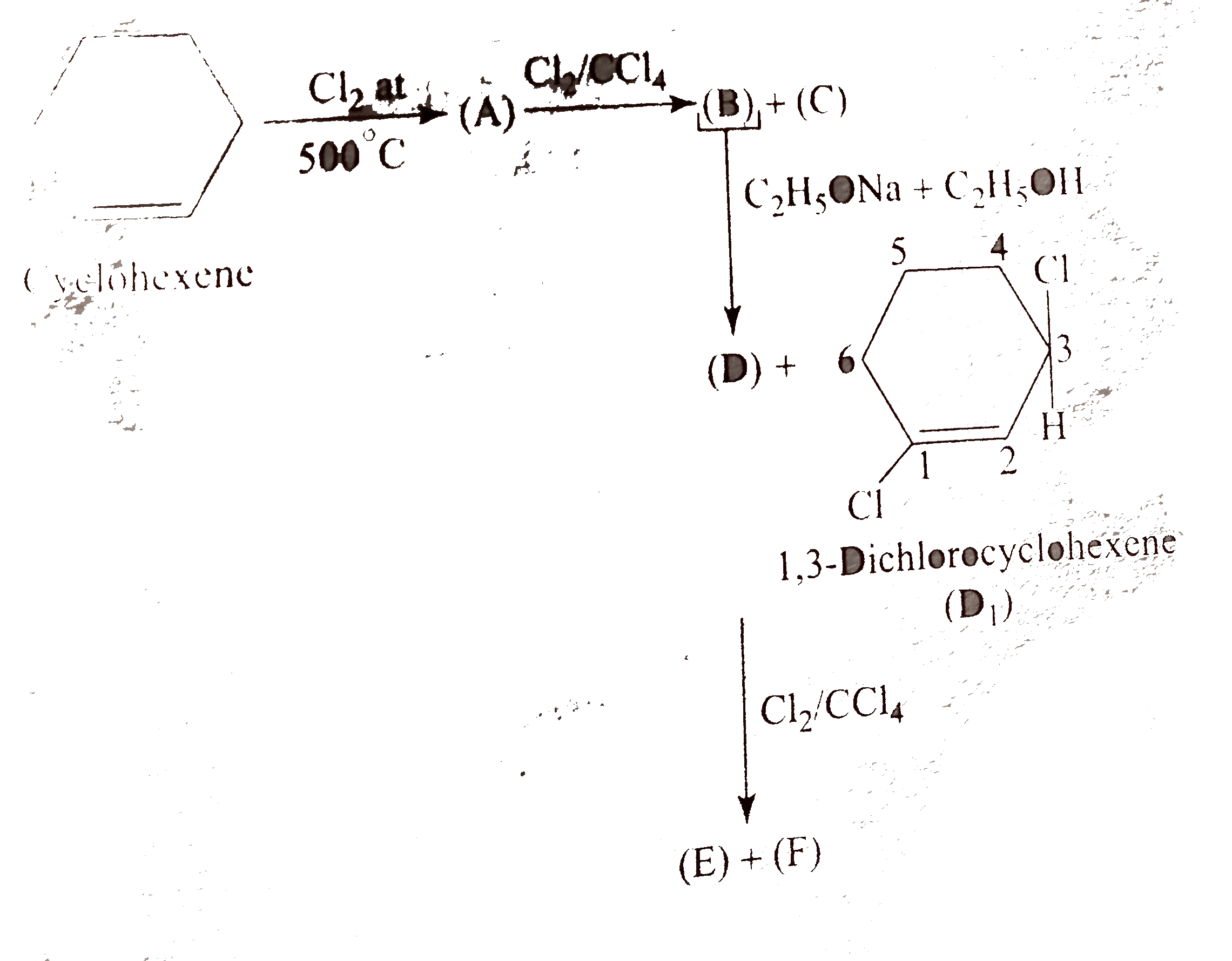
(E) and (F), respectively, are :
View SolutionIf F0 andFe are the focal lengths of the objective and eye-piece respectively for a Galilean telescope, its magnifying power is about
View SolutionTwo small conducting spheres of equal radius have charges +10μC and −20μC respectively and placed at a distance R from each other. They experience force F1. If they are brought in contact and separated to the same distance, they experience force F2. The ratio of F1 to F2 is
View SolutionThe force of repulsion between two electrons at a certain distance is F. The force between two protons separated by the same distance is (mp=1836me)
View SolutionA block pulley arrangement is shown in the figure. If f1andf2 represents frictional force acting on the block A and B respectively then choose the correct statement. (given g=10m/s2)
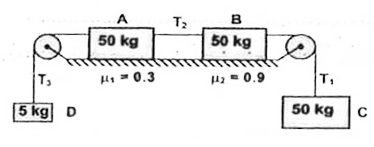
View SolutionIn a compound microscope the objective of fo and eyepiece of fe are placed at distance L such that L equals
View SolutionFpp,FnnandFnp are the nuclear forces between proton - proton , neutron - neutron and neutron - proton respectively . Then relation between them is
View SolutionThree long wires are situated in a plane with equal separation. A current of 1A, 2A, 3A flows through these wires in the same direction. What is ratio of F1/F2? Where F1 & F2 are force per unit length on the wire 1 and 2 respectively:
View Solution
