The inward and outward electric flux for a closed surface unit of are respectively and . Then the total charge inside the surface is [where permittivity constant]
The correct Answer is:D
To solve the problem, we will use Gauss's law, which states that the net electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (ε₀).
1. Identify Given Values:
- Inward electric flux (Φ_in) = -8 × 10³ N·m²/C (considered negative)
- Outward electric flux (Φ_out) = +4 × 10³ N·m²/C (considered positive)
2. Calculate Net Electric Flux:
The net electric flux (Φ_net) through the closed surface is the sum of the inward and outward flux:
Φnet=Φout+Φin
Substituting the values:
Φnet=4×10³+(−8×10³)=4×10³−8×10³=−4×10³N⋅m²/C
3. Apply Gauss's Law:
According to Gauss's law:
Φnet=Qenclosedε₀
Rearranging gives:
Qenclosed=Φnet×ε₀
4. Substitute the Net Flux:
Now substituting the value of Φ_net:
Qenclosed=(−4×10³)×ε₀
5. Final Expression for Charge:
Thus, the total charge inside the surface is:
Qenclosed=−4×10³ε₀C
Conclusion:
The total charge inside the surface is −4×10³ε₀C.
- Inward electric flux (Φ_in) = -8 × 10³ N·m²/C (considered negative)
- Outward electric flux (Φ_out) = +4 × 10³ N·m²/C (considered positive)
The net electric flux (Φ_net) through the closed surface is the sum of the inward and outward flux:
Φnet=Φout+Φin
Substituting the values:
Φnet=4×10³+(−8×10³)=4×10³−8×10³=−4×10³N⋅m²/C
According to Gauss's law:
Φnet=Qenclosedε₀
Rearranging gives:
Qenclosed=Φnet×ε₀
Now substituting the value of Φ_net:
Qenclosed=(−4×10³)×ε₀
Thus, the total charge inside the surface is:
Qenclosed=−4×10³ε₀C
The total charge inside the surface is −4×10³ε₀C.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Taking it together
105 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
View SolutionA closed surface encloses a net charge of −3.60μC. What is the net electric flux through the surface?
(b) The electric flux through a closed surface is found to be 780N−m2/C. What quantity of charge is enclosed by the surface?
(c) The closed surface in part (b) is a cube with sides of length 2.50 cm. From the information given in part (b), is it possible to tell where within the cube the charge is located? Explain.
View SolutionThe electric potential on the surface of a sphere of radius R and charge 3×10−6 C is 500 V The intensity of electric field on the surface of the sphere ( inNC−1) is
View SolutionCareful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0×103Nm2/C (a) what is the net charge inside the box ? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box ? Why or why not?
View SolutionSurface charge density of a sphere of a radius 10 cm is 8.85×10−8c/m2. Potential at the centre of the sphere is
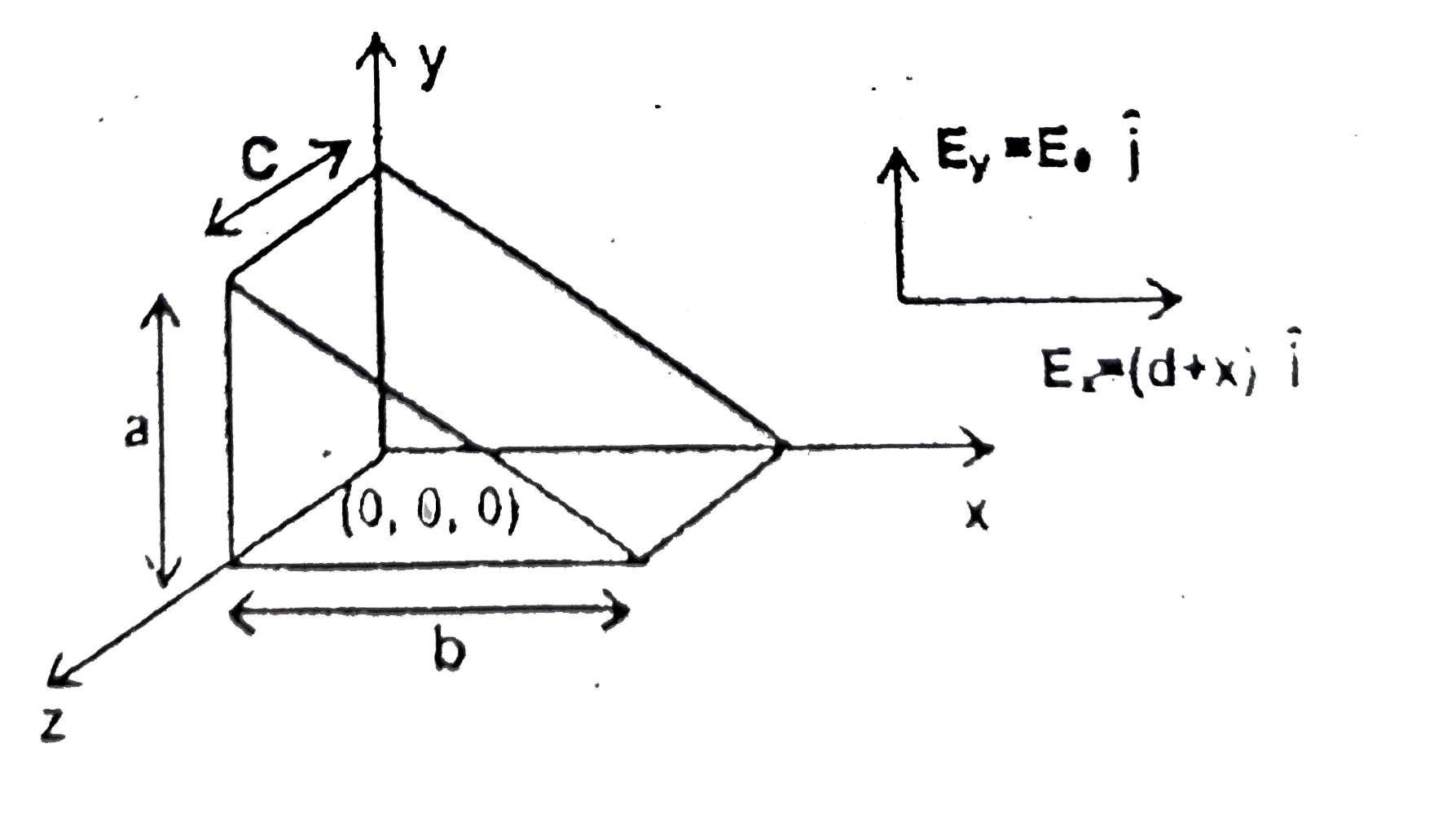
View SolutionIn the given electric field →E=[(d+x)ˆi+E0ˆj]N/Ca hypothetical closed surface is taken as shown in figure. The total charge enclosed within the closed surface is Kε0. Then, find the value of k. (a=2m, b=3m and c=2m)
View SolutionThe electric force experienced by a charge of 5×10−6C is 25×10−3N. Find the magnitude of the electric field at that position of the charge due to the source charges.
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionThe force experienced by a charge of 2μC in an electric field is 3×10−3N. The intensity of the electric field.
View Solution
