Two equal and opposite charges of masses m1 and m2 are accelerated in a uniform electric field through the same distance. What is the ratio of their accelerations, if their ratio of masses is m1m2=0.5?
a1a2=0.5
a1a2=1
a1a2=2
a1a2=3
The correct Answer is:C
To solve the problem, we need to find the ratio of the accelerations of two equal and opposite charges with given masses m1 and m2, where the ratio of their masses is m1m2=0.5.
1. Understanding the Forces:
The force acting on a charged particle in an electric field E is given by:
F=Q⋅E
where Q is the charge. For the two charges, we can denote them as Q1=+Q and Q2=−Q.
2. Applying Newton's Second Law:
According to Newton's second law, the force can also be expressed as:
F=m⋅a
Therefore, for the first charge (mass m1):
F1=m1⋅a1=Q⋅E
And for the second charge (mass m2):
F2=m2⋅a2=−Q⋅E
3. Setting Up the Equations:
From the equations above, we can express the accelerations a1 and a2:
a1=Q⋅Em1
a2=−Q⋅Em2
4. Finding the Ratio of Accelerations:
To find the ratio a1a2:
a1a2=Q⋅Em1−Q⋅Em2=m2m1
The negative sign indicates the direction of acceleration is opposite, but for the ratio, we are interested in the magnitudes.
5. Using the Given Mass Ratio:
We know from the problem that:
m1m2=0.5⟹m2=m10.5=2m1
Therefore:
m2m1=2
6. Final Calculation:
Substituting back into the ratio of accelerations:
a1a2=m2m1=2
Conclusion:
The ratio of the accelerations a1a2 is 2.
The force acting on a charged particle in an electric field E is given by:
F=Q⋅E
where Q is the charge. For the two charges, we can denote them as Q1=+Q and Q2=−Q.
According to Newton's second law, the force can also be expressed as:
F=m⋅a
Therefore, for the first charge (mass m1):
F1=m1⋅a1=Q⋅E
And for the second charge (mass m2):
F2=m2⋅a2=−Q⋅E
From the equations above, we can express the accelerations a1 and a2:
a1=Q⋅Em1
a2=−Q⋅Em2
To find the ratio a1a2:
a1a2=Q⋅Em1−Q⋅Em2=m2m1
The negative sign indicates the direction of acceleration is opposite, but for the ratio, we are interested in the magnitudes.
We know from the problem that:
m1m2=0.5⟹m2=m10.5=2m1
Therefore:
m2m1=2
Substituting back into the ratio of accelerations:
a1a2=m2m1=2
The ratio of the accelerations a1a2 is 2.
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Match the columns
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
Similar Questions
Two particles of mass m and 2m with charges 2q and q are placed in a uniform electric field E and allowed to move for same time. Find the ratio of their kinetic energie
View SolutionTwo bodies of masses m1 and m2 have equal KE. Their momenta is in the ratio
View SolutionTwo particles of masses m and 2m and charges 2q and q are placed in a uniform electric field E and allowed to move for the same time. The ratio of kinetic energies will be -
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View SolutionTwo bodies of masses m1andm2 have same kinetic energy. The ratio of their momentum is
View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
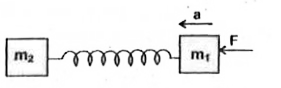
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View Solution