Two capacitors of capacitance and are joined in series. Outer plate first capacitor is at volt and outer plate of second capacitor is earthed (grounded). Now the potential on inner plate of each capacitor will be
700 V
200 V
600 V
400 V
The correct Answer is:D
To find the potential on the inner plates of two capacitors connected in series, we can follow these steps:
Step 1: Understand the Configuration
We have two capacitors:
- Capacitor 1 (C1) = 2 µF
- Capacitor 2 (C2) = 3 µF
They are connected in series, with the outer plate of C1 at 1000 V and the outer plate of C2 grounded (0 V).
Step 2: Use the Concept of Series Capacitors
In a series connection, the charge (Q) on each capacitor is the same. The potential difference across each capacitor can be expressed as:
- V1=QC1
- V2=QC2
The total voltage across the series combination is the sum of the voltages across each capacitor:
Vtotal=V1+V2
Step 3: Write the Voltage Equations
Given that the outer plate of C1 is at 1000 V and the outer plate of C2 is at 0 V, we can express the total voltage as:
1000V−V1=V2−0V
Thus, we can write:
V1+V2=1000
Step 4: Relate Voltages to Charges
From the equations of voltage across the capacitors, we can substitute V1 and V2:
V1=QC1=Q2×10−6
V2=QC2=Q3×10−6
Step 5: Substitute and Solve
Substituting these into the total voltage equation:
Q2×10−6+Q3×10−6=1000
To solve for Q, we first find a common denominator:
3Q+2Q6×10−6=1000
5Q6×10−6=1000
Now, multiply both sides by 6×10−6:
5Q=1000×6×10−6
5Q=6×10−3
Q=6×10−35=1.2×10−3C
Step 6: Calculate the Voltages
Now, we can find V1 and V2:
V1=QC1=1.2×10−32×10−6=600V
V2=QC2=1.2×10−33×10−6=400V
Step 7: Find the Potential on Inner Plates
The potential on the inner plate of C1 (V1) is 600 V, and the potential on the inner plate of C2 (V2) is 400 V.
Final Answer
- The potential on the inner plate of the first capacitor (C1) is 600 V.
- The potential on the inner plate of the second capacitor (C2) is 400 V.
We have two capacitors:
- Capacitor 1 (C1) = 2 µF
- Capacitor 2 (C2) = 3 µF
In a series connection, the charge (Q) on each capacitor is the same. The potential difference across each capacitor can be expressed as:
- V1=QC1
- V2=QC2
Vtotal=V1+V2
Given that the outer plate of C1 is at 1000 V and the outer plate of C2 is at 0 V, we can express the total voltage as:
1000V−V1=V2−0V
Thus, we can write:
V1+V2=1000
From the equations of voltage across the capacitors, we can substitute V1 and V2:
V1=QC1=Q2×10−6
V2=QC2=Q3×10−6
Substituting these into the total voltage equation:
Q2×10−6+Q3×10−6=1000
3Q+2Q6×10−6=1000
5Q6×10−6=1000
5Q=1000×6×10−6
5Q=6×10−3
Q=6×10−35=1.2×10−3C
Now, we can find V1 and V2:
V1=QC1=1.2×10−32×10−6=600V
V2=QC2=1.2×10−33×10−6=400V
The potential on the inner plate of C1 (V1) is 600 V, and the potential on the inner plate of C2 (V2) is 400 V.
- The potential on the inner plate of the first capacitor (C1) is 600 V.
- The potential on the inner plate of the second capacitor (C2) is 400 V.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises227videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises17videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.415videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
Two capacitors of 2μF and 3μF are connected in series. The potential at point A is 1000 volt and the outer plate of 3μF capacitor is earthed. The potential at point B is
View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View Solution
Knowledge Check
- Question 1 - Select One
The potential difference between points A and B is
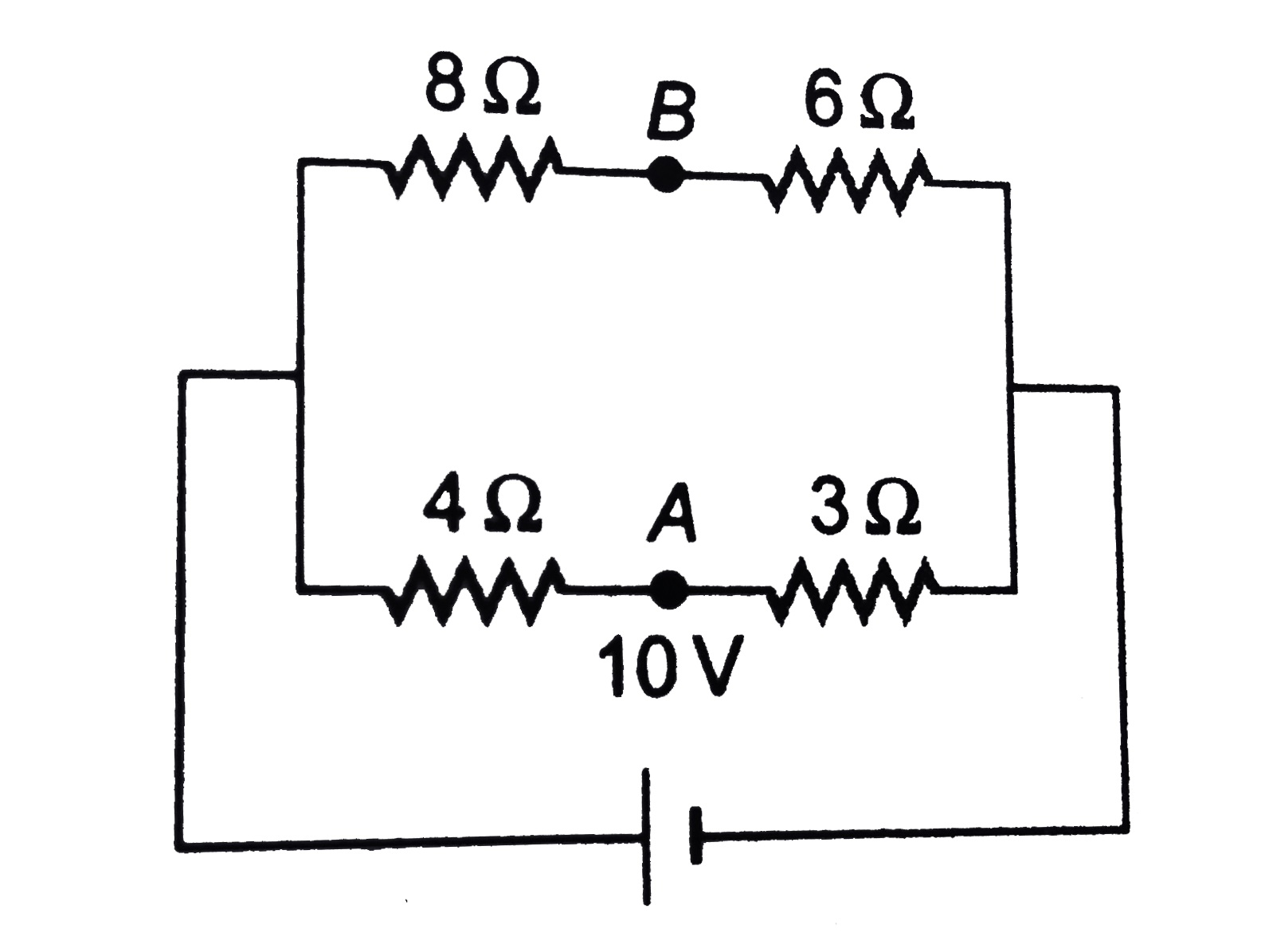A2B5C11D18
Two capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View SolutionThree capcaitors of capacities 1μF,2μF and 3μF are charged by 10V,20V and 30V respectively. Now positive plates of first two capacitors are connected with the negative plate of third capacitor on one side and negative plates of first wo capacitors are connectes with positive of third capacitor on the other side. Find
a. common potential V
b. final charges on different capacitors.View SolutionThree capacitors 2μF,3μFand6μF are joined with each other. What is the minimum effective capacitance?
View Solution