A parallel plate capacitor is made by stacking n equally spaced plates connected alternatively. If the capacitance between any two adjacent plates is 'C' then the resultant capacitance is
C
nC
(n−1)C
(n+1)C
The correct Answer is:C
To solve the problem of finding the resultant capacitance of a parallel plate capacitor made by stacking n equally spaced plates connected alternatively, we can follow these steps:
1. Understanding the Configuration:
- We have n plates arranged in such a way that they are connected alternatively. This means that if we label the plates as P1, P2, P3, ..., Pn, then P1 is connected to P2, P3 is connected to P4, and so on.
2. Identifying Capacitors:
- The capacitance is defined between adjacent plates. Therefore, the capacitors formed will be:
- C1 between P1 and P2,
- C2 between P2 and P3,
- C3 between P3 and P4,
- ...,
- C(n-1) between P(n-1) and Pn.
3. Counting the Capacitors:
- Since there are n plates, the number of capacitors formed will be (n - 1). This is because each pair of adjacent plates forms one capacitor.
4. Capacitance of Each Capacitor:
- Each of these capacitors has a capacitance of C.
5. Calculating the Total Capacitance:
- Since all the capacitors are connected in parallel between the two points (let's call them A and B), the total capacitance (C_eq) can be calculated by simply adding the capacitances of the individual capacitors.
- Therefore, the equivalent capacitance is given by:
Ceq=(n−1)⋅C
Final Result:
The resultant capacitance between the two points A and B is:
Ceq=(n−1)C
- We have n plates arranged in such a way that they are connected alternatively. This means that if we label the plates as P1, P2, P3, ..., Pn, then P1 is connected to P2, P3 is connected to P4, and so on.
- The capacitance is defined between adjacent plates. Therefore, the capacitors formed will be:
- C1 between P1 and P2,
- C2 between P2 and P3,
- C3 between P3 and P4,
- ...,
- C(n-1) between P(n-1) and Pn.
- Since there are n plates, the number of capacitors formed will be (n - 1). This is because each pair of adjacent plates forms one capacitor.
- Each of these capacitors has a capacitance of C.
- Since all the capacitors are connected in parallel between the two points (let's call them A and B), the total capacitance (C_eq) can be calculated by simply adding the capacitances of the individual capacitors.
- Therefore, the equivalent capacitance is given by:
Ceq=(n−1)⋅C
The resultant capacitance between the two points A and B is:
Ceq=(n−1)C
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A parallel plate capacitor has 91 plates, all are identical and arranged with same spacing between them. If the capacitance between adjacent plates is 3 pF. What will be the resultant capacitance?
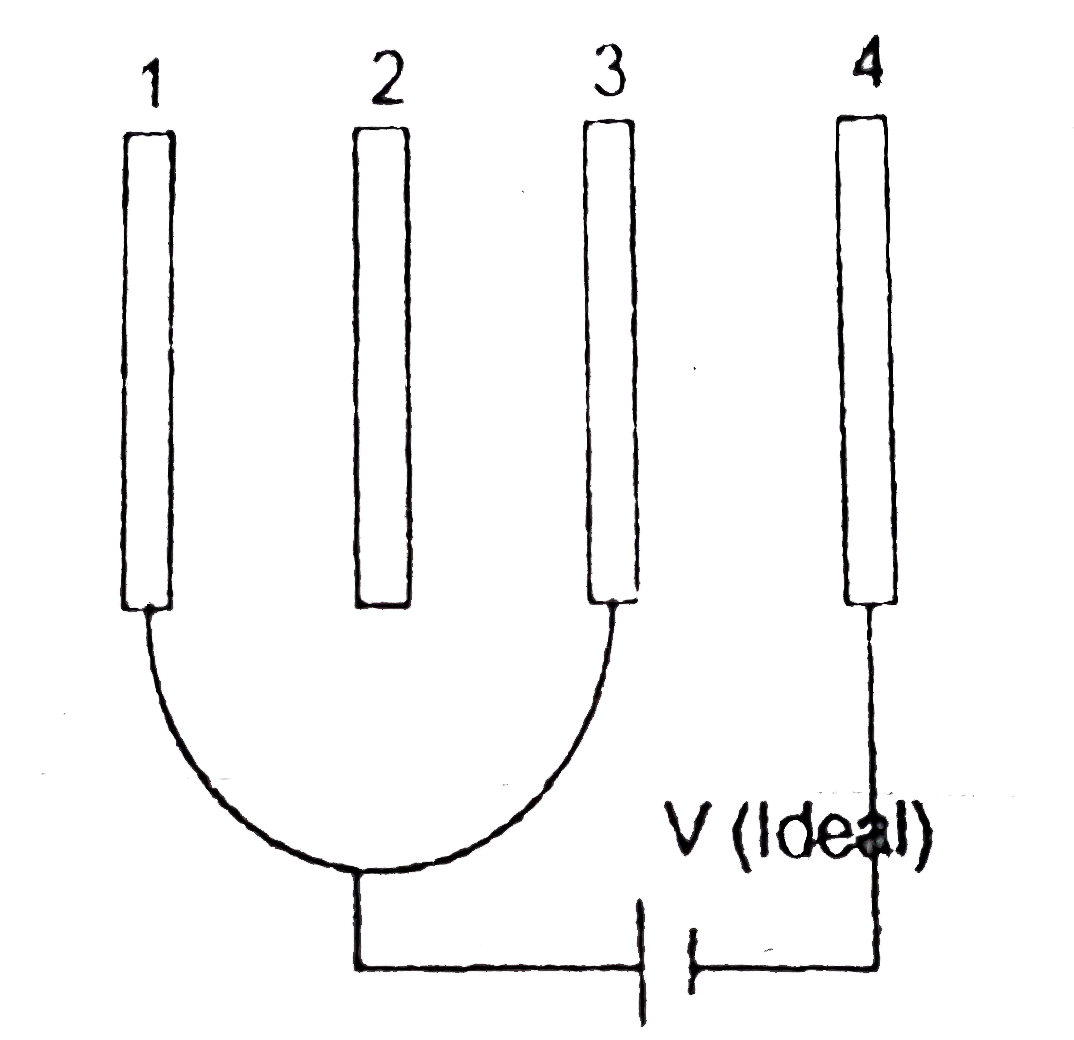
View SolutionFour identical paltes (equally spaced) and a battery are connected as shown. If the capacitance between two consecutive plates is C then choose the correct statement
View Solution
Knowledge Check
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF
In a parallel plate capacitor with air between the plates, each plate has an area of 6×10−3m2 and distance between the plates is 3mm. Calculate the capacitance. If this capacitance is connected to a 100V supply, what is the charge on each plate of the capacitor ?
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionIf the plates of a parallel plate capacitor are not equal in area, then
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionTwo parallel plate vacuum capacitors have areas A1 and A2 and equal plate spacing d. Show that when the capacitors are connected in parallel, the equivalent capacitance is the same as for a single capacitor with plate area A1+A2 and spacing d.
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

View SolutionA parallel plate capacitor is charged by a battery, which is then disconnected. A dielectric slab is now introduced between the two plates to occupy the space completely. State the effect on the following:
(i) the capacitance of the capacitor.
(ii) potential difference between the plates.
(iii) the energy stored in the capacitor.
View Solution
