If the charge on a capacitorn is increased by 2C, then the energy stored in it increases by 21 %. The original charge on the capacitor is
10 C
20 C
30 C
40 C
The correct Answer is:B
To solve the problem, we need to determine the original charge on the capacitor given that an increase of 2C in charge results in a 21% increase in the energy stored in the capacitor.
1. Understanding the Energy Stored in a Capacitor:
The energy (U) stored in a capacitor can be expressed as:
U=12Q2C
where Q is the charge on the capacitor and C is the capacitance.
2. Initial Energy:
Let the initial charge on the capacitor be Q. The initial energy stored in the capacitor is:
Ui=12Q2C
3. Final Charge and Energy:
When the charge is increased by 2C, the new charge becomes Q+2. The energy stored in the capacitor now is:
Uf=12(Q+2)2C
4. Energy Increase:
According to the problem, the energy increases by 21%. Therefore:
Uf=Ui+0.21Ui=1.21Ui
5. Setting Up the Equation:
Now, we can set up the equation:
12(Q+2)2C=1.21(12Q2C)
We can cancel 12C from both sides:
(Q+2)2=1.21Q2
6. Expanding and Rearranging:
Expanding the left side:
Q2+4Q+4=1.21Q2
Rearranging gives:
4Q+4=1.21Q2−Q2
4Q+4=0.21Q2
Rearranging further:
0.21Q2−4Q−4=0
7. Using the Quadratic Formula:
We can solve this quadratic equation using the quadratic formula:
Q=−b±√b2−4ac2a
Here, a=0.21, b=−4, and c=−4:
Q=4±√(−4)2−4⋅0.21⋅(−4)2⋅0.21
=4±√16+3.360.42
=4±√19.360.42
=4±4.40.42
8. Calculating the Values:
This gives us two potential solutions:
Q=8.40.42orQ=−0.40.42
The negative value is not physically meaningful, so we take:
Q=20 C
Final Answer:
The original charge on the capacitor is Q=20 C.
---
The energy (U) stored in a capacitor can be expressed as:
U=12Q2C
where Q is the charge on the capacitor and C is the capacitance.
Let the initial charge on the capacitor be Q. The initial energy stored in the capacitor is:
Ui=12Q2C
When the charge is increased by 2C, the new charge becomes Q+2. The energy stored in the capacitor now is:
Uf=12(Q+2)2C
According to the problem, the energy increases by 21%. Therefore:
Uf=Ui+0.21Ui=1.21Ui
Now, we can set up the equation:
12(Q+2)2C=1.21(12Q2C)
We can cancel 12C from both sides:
(Q+2)2=1.21Q2
Expanding the left side:
Q2+4Q+4=1.21Q2
Rearranging gives:
4Q+4=1.21Q2−Q2
4Q+4=0.21Q2
Rearranging further:
0.21Q2−4Q−4=0
We can solve this quadratic equation using the quadratic formula:
Q=−b±√b2−4ac2a
Here, a=0.21, b=−4, and c=−4:
Q=4±√(−4)2−4⋅0.21⋅(−4)2⋅0.21
=4±√16+3.360.42
=4±√19.360.42
=4±4.40.42
This gives us two potential solutions:
Q=8.40.42orQ=−0.40.42
The negative value is not physically meaningful, so we take:
Q=20 C
The original charge on the capacitor is Q=20 C.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Find the charge stored in the capacitor.
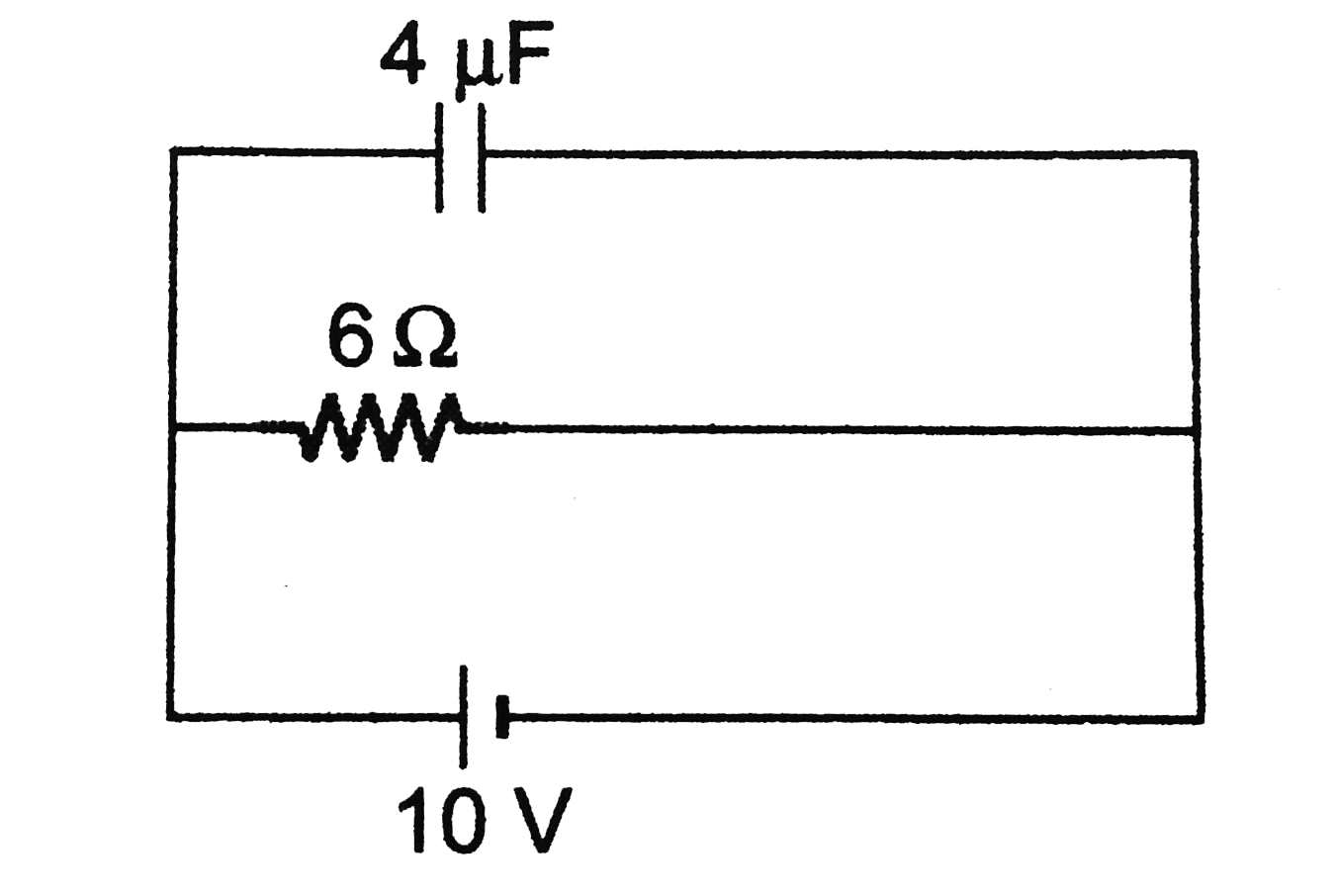
View SolutionFind the charge stored in the capacitor.
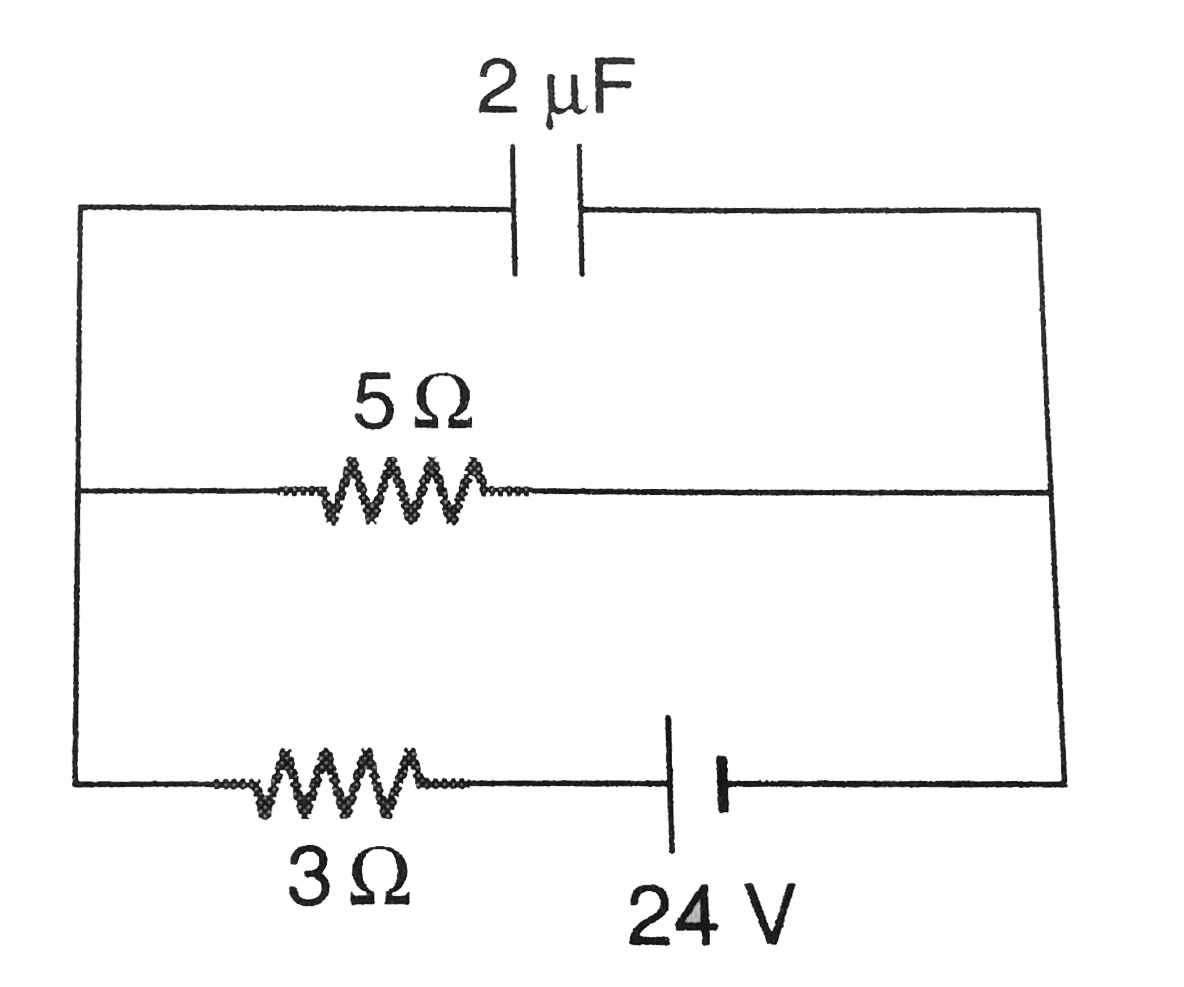
View SolutionFind the charge stored in the capacitor.
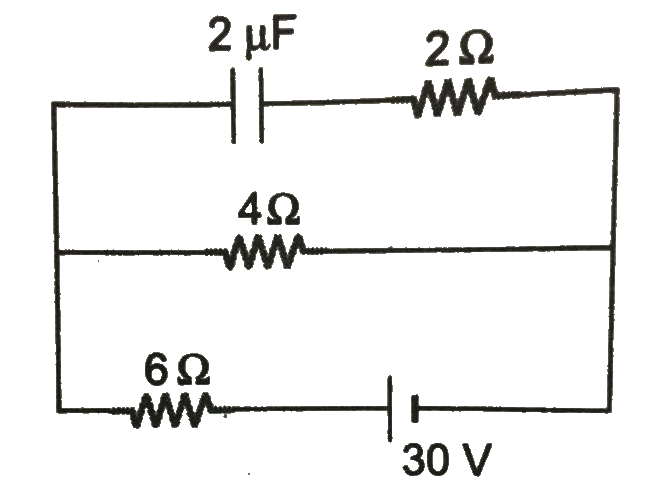
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionIf height of transmitting tower increases by 21% then the area to be covered increases by
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionFind the charged stored in all the capacitors
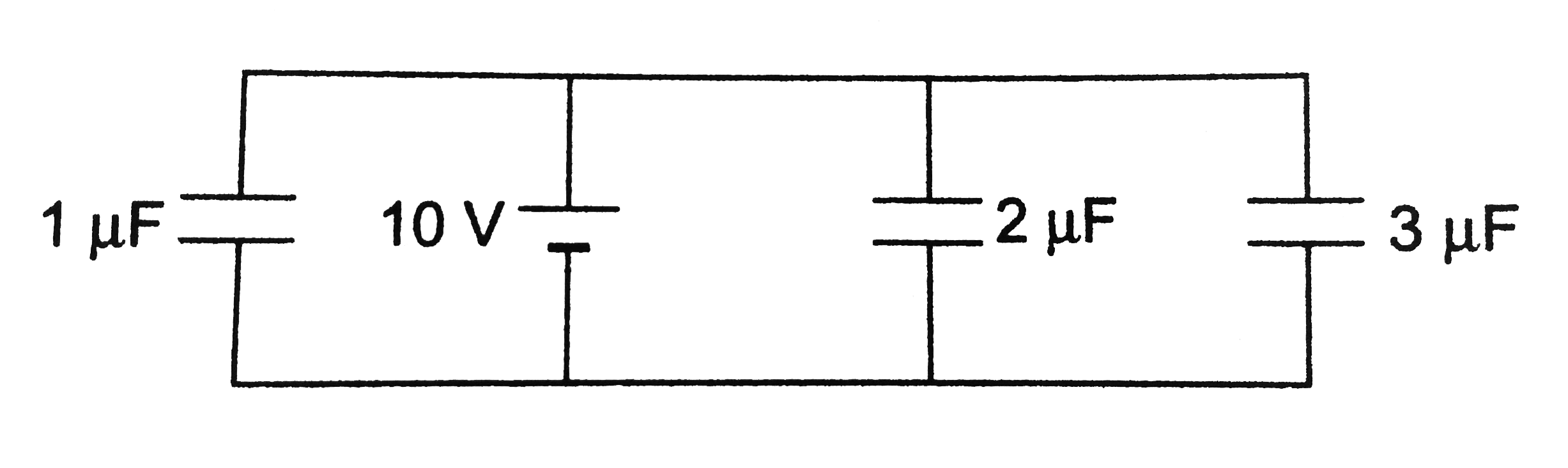
View SolutionIn a charged capacitor, the energy resides in
View SolutionA parallel plate capacitor of capacitane C is charged to a potential V. It is then connected to another uncharged capacitor with the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100V?
View Solution
