A variable condenser is permanently connect to a 100V battery. If the capacity is charged from 2μF to 10μF, then change in energy is equal to
2×10−2J
2.5×10−2J
3.5×10−2J
4×10−2J
The correct Answer is:D
To find the change in energy of a variable condenser connected to a 100V battery when the capacitance changes from 2μF to 10μF, we can follow these steps:
Step 1: Understand the formula for energy stored in a capacitor
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
where:
- U is the energy stored,
- C is the capacitance,
- V is the voltage across the capacitor.
Step 2: Calculate the initial energy with C1=2μF
Given:
- C1=2μF=2×10−6F
- V=100V
Using the formula:
U1=12C1V2
U1=12×(2×10−6)×(100)2
U1=12×(2×10−6)×10000
U1=12×2×10−2
U1=1×10−2J
U1=0.01J
Step 3: Calculate the final energy with C2=10μF
Given:
- C2=10μF=10×10−6F
Using the formula:
U2=12C2V2
U2=12×(10×10−6)×(100)2
U2=12×(10×10−6)×10000
U2=12×10×10−2
U2=5×10−2J
U2=0.05J
Step 4: Calculate the change in energy
The change in energy (ΔU) is given by:
ΔU=U2−U1
ΔU=0.05J−0.01J
ΔU=0.04J
Final Answer
The change in energy is:
ΔU=0.04J
---
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
where:
- U is the energy stored,
- C is the capacitance,
- V is the voltage across the capacitor.
Given:
- C1=2μF=2×10−6F
- V=100V
U1=12C1V2
U1=12×(2×10−6)×(100)2
U1=12×(2×10−6)×10000
U1=12×2×10−2
U1=1×10−2J
U1=0.01J
Given:
- C2=10μF=10×10−6F
U2=12C2V2
U2=12×(10×10−6)×(100)2
U2=12×(10×10−6)×10000
U2=12×10×10−2
U2=5×10−2J
U2=0.05J
The change in energy (ΔU) is given by:
ΔU=U2−U1
ΔU=0.05J−0.01J
ΔU=0.04J
The change in energy is:
ΔU=0.04J
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
If the potential of a capacitor having capacity of 6μF is increased from 10 V to 20 V,then increase in its energy will be
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionAn RC− circuit, with R=600kΩ and C=10μF, is connected to a 5.0−V battery unit the capacitor is fully charged. Then, the battery is suddenly replaced with a new 3.00−V battery of opposite polarity. At what time after this replacement will the energy stored in the capacitor be zero ? (given that e≈83 )
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?

View SolutionA capacitor of capacitance value 1μF is charged to 30 V and the battery is then disconnected. If it is connected across a 2μF capacotor, then the energy lost by the system is
View SolutionThree capacitors C1,C2,andC3 of capacitance 1μF,2μF,and3μF, respectively, are charged separately as shown in the figure. Now these charged capacitors are connected to a battery of ε=20V and an uncharged capacitor of C=2μF as shown in figure.
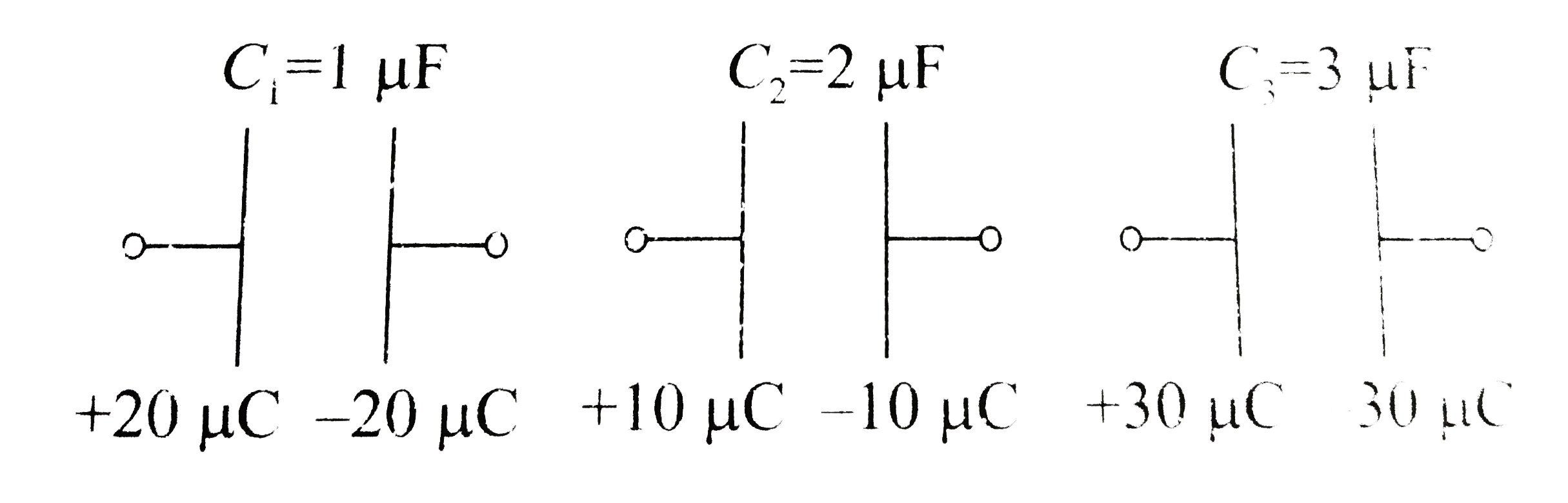 ,
, 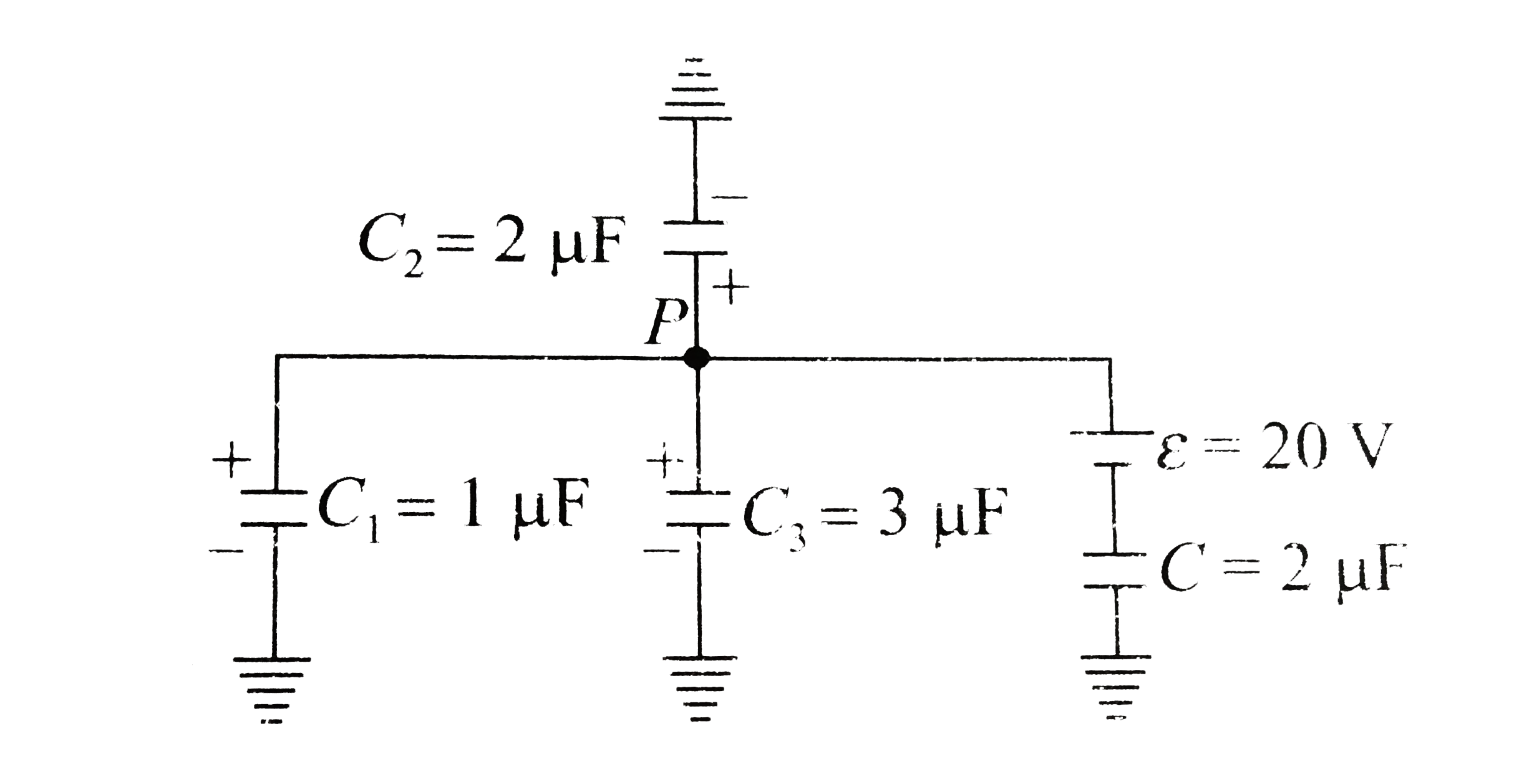
The charge on capacitor marked C is
View SolutionA condenser of capacity 16 mF charged to a potential of 20 V is connected to a condenser of capacity C charged to a potential of 10 V as shown in the figure.

If the common potential is 14 V. the capacity C is equal to
View SolutionA capacitor 4μF charged to 50V is connected to another capacitor of 2μF charged to 100V with plates of like charges connected together. The total energy before and after connection in multiples of (10−2J) is
View SolutionThree capacitors C1,C2,andC3 of capacitance 1μF,2μF,and3μF, respectively, are charged separately as shown in the figure. Now these charged capacitors are connected to a battery of ε=20V and an uncharged capacitor of C=2μF as shown in figure.
 ,
, 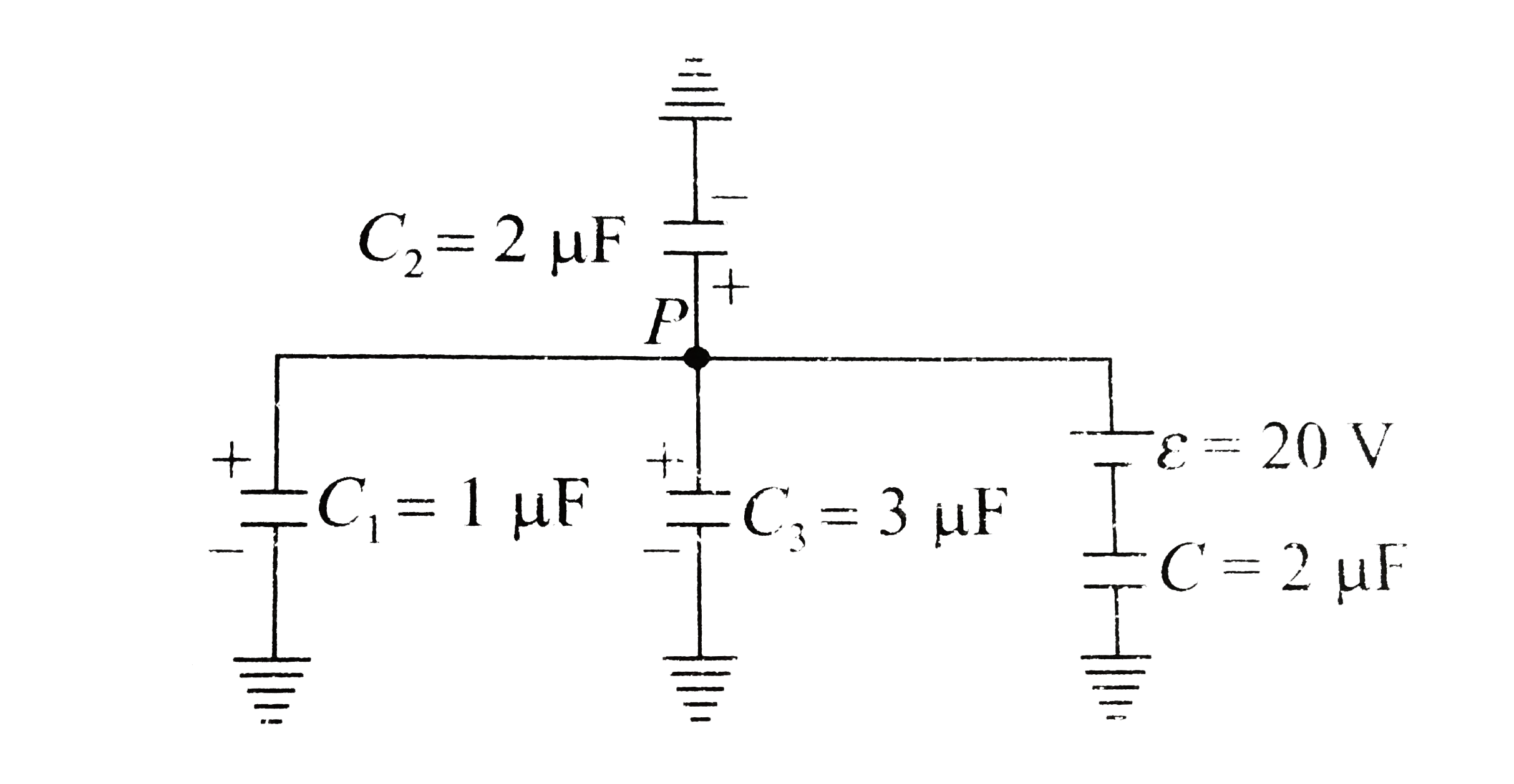
The potential of point P is
View SolutionThree condensers of same capacity connected in series has effective capacity 2mF. If they are connected in parallel and charged using a battery of emf 12V, the total energy stored in the combination is
View Solution
