How many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
990
900
9090
909
The correct Answer is:C
To solve the problem of how many 1 µF capacitors must be connected in parallel to store a charge of 1C with a potential of 110V across the capacitors, we can follow these steps:
Step 1: Understand the relationship between charge, capacitance, and voltage
The relationship between charge (Q), capacitance (C), and voltage (V) is given by the formula:
\( Q = C \times V \)
Step 2: Determine the equivalent capacitance for capacitors in parallel
When capacitors are connected in parallel, the equivalent capacitance (C_eq) is the sum of the individual capacitances. If we have n capacitors each of capacitance C, then:
\( C_{eq} = n \times C \)
Step 3: Substitute the values into the formula
We know:
- The charge \( Q = 1 \, C \)
- The voltage \( V = 110 \, V \)
- The capacitance of each capacitor \( C = 1 \, \mu F = 1 \times 10^{-6} \, F \)
Substituting these values into the charge formula:
\( Q = C_{eq} \times V \)
\( 1 = (n \times 1 \times 10^{-6}) \times 110 \)
Step 4: Solve for n
Rearranging the equation to solve for \( n \):
\( n = \frac{Q}{C_{eq} \times V} \)
\( n = \frac{1}{(1 \times 10^{-6}) \times 110} \)
Calculating the denominator:
\( n = \frac{1}{1.1 \times 10^{-4}} \)
\( n = \frac{1}{1.1} \times 10^{4} \)
\( n \approx 9.09 \times 10^{3} \)
Since \( n \) must be a whole number, we round it up to the nearest whole number:
\( n \approx 9091 \)
Step 5: Conclusion
Therefore, approximately 9091 capacitors of 1µF must be connected in parallel to store a charge of 1C with a potential of 110V across the capacitors.
---
The relationship between charge (Q), capacitance (C), and voltage (V) is given by the formula:
\( Q = C \times V \)
When capacitors are connected in parallel, the equivalent capacitance (C_eq) is the sum of the individual capacitances. If we have n capacitors each of capacitance C, then:
\( C_{eq} = n \times C \)
We know:
- The charge \( Q = 1 \, C \)
- The voltage \( V = 110 \, V \)
- The capacitance of each capacitor \( C = 1 \, \mu F = 1 \times 10^{-6} \, F \)
\( Q = C_{eq} \times V \)
\( 1 = (n \times 1 \times 10^{-6}) \times 110 \)
Rearranging the equation to solve for \( n \):
\( n = \frac{Q}{C_{eq} \times V} \)
\( n = \frac{1}{(1 \times 10^{-6}) \times 110} \)
\( n = \frac{1}{1.1 \times 10^{-4}} \)
\( n = \frac{1}{1.1} \times 10^{4} \)
\( n \approx 9.09 \times 10^{3} \)
\( n \approx 9091 \)
Therefore, approximately 9091 capacitors of 1µF must be connected in parallel to store a charge of 1C with a potential of 110V across the capacitors.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
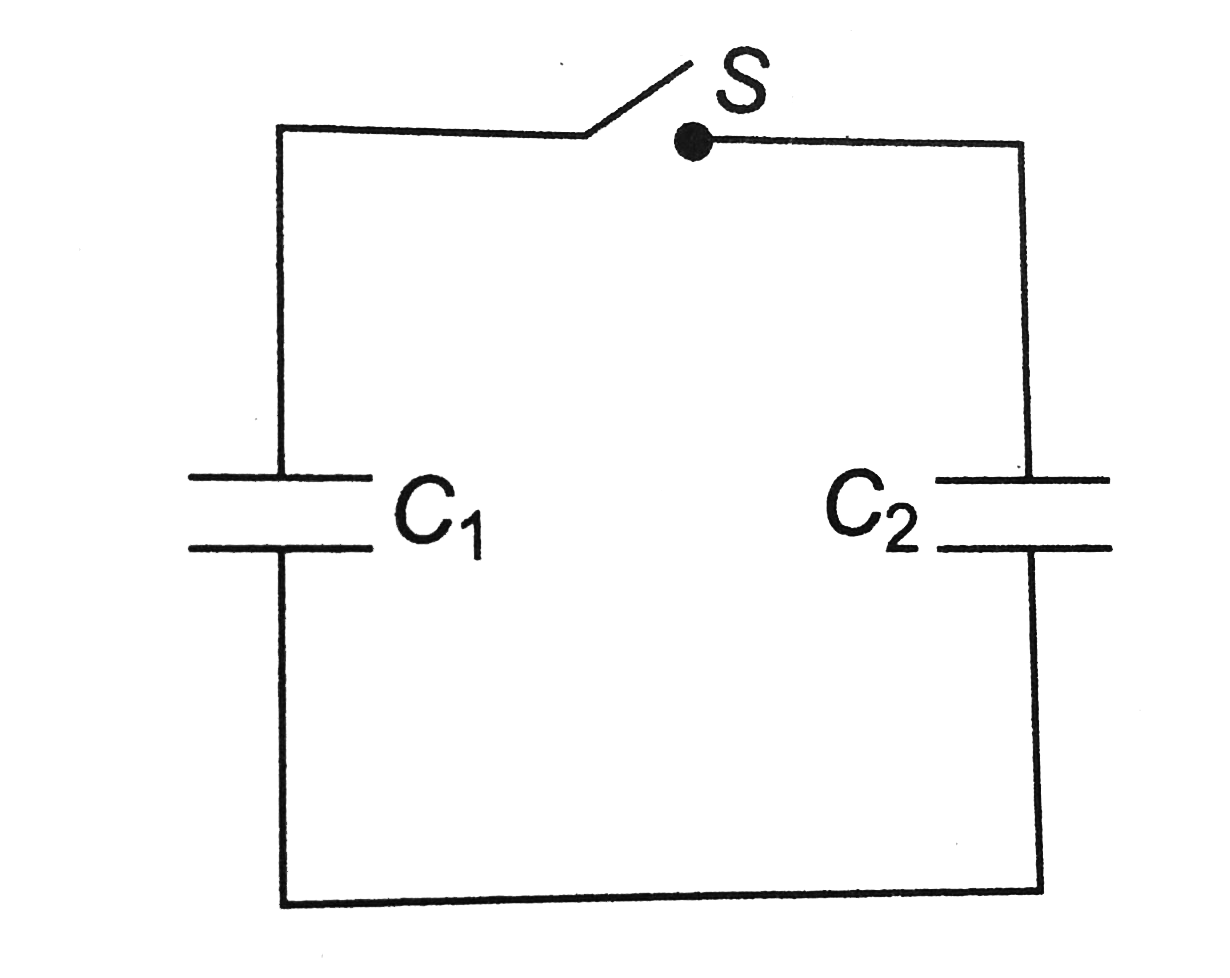
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
The potential drop across 7μF capacitor is 6V. Then
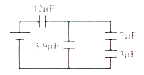
View SolutionA resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate the capacity of second capacitor.
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100V?
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ? If another capacitor of 6 pF is connected across the combination, find the charge stored and potential difference across each capacitor.
View Solution