Assertion : Five charges +q each are placed at five vertices of a regular pentagon. A sixth xharge −Q is placed at the centre of pentagon. Then, net electrostatic force on −Q is zero.
Reason : Net electrostatic potential at the centre is zero.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:C
To solve the question, we need to analyze the assertion and reason provided:
Assertion:
Five charges +q each are placed at five vertices of a regular pentagon. A sixth charge −Q is placed at the center of the pentagon. Then, the net electrostatic force on −Q is zero.
Reason:
Net electrostatic potential at the center is zero.
1. Understanding the Configuration:
- We have five positive charges +q located at the vertices of a regular pentagon.
- A negative charge −Q is placed at the center of the pentagon.
2. Analyzing the Forces on Charge −Q:
- Each positive charge +q exerts an attractive force on the negative charge −Q.
- Due to the symmetry of the pentagon, the forces exerted by the five charges on −Q will be equal in magnitude but will act in different directions.
3. Symmetry and Resultant Force:
- The five forces will be symmetrically distributed around the center.
- Since the angles between the lines connecting the center to each vertex are equal (72 degrees), the resultant force on the charge −Q will be zero.
- Thus, the assertion is true: the net electrostatic force on −Q is zero.
4. Calculating the Electrostatic Potential:
- The electrostatic potential V at a point due to a point charge is given by the formula:
\(
V = k \frac{q}{r}
\)
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point of interest.
- For the charge −Q at the center, the potential due to each +q charge is the same, and since there are five such charges, the total potential at the center is:
\(
V_{\text{total}} = 5 \cdot k \frac{q}{r}
\)
- This potential is non-zero because it is a scalar quantity and adds up.
5. Conclusion:
- The assertion is true, but the reason is false. The net electrostatic potential at the center is not zero; it is a non-zero value due to the presence of the five positive charges.
Final Answer:
- Assertion: True
- Reason: False
Five charges +q each are placed at five vertices of a regular pentagon. A sixth charge −Q is placed at the center of the pentagon. Then, the net electrostatic force on −Q is zero.
Net electrostatic potential at the center is zero.
- We have five positive charges +q located at the vertices of a regular pentagon.
- A negative charge −Q is placed at the center of the pentagon.
- Each positive charge +q exerts an attractive force on the negative charge −Q.
- Due to the symmetry of the pentagon, the forces exerted by the five charges on −Q will be equal in magnitude but will act in different directions.
- The five forces will be symmetrically distributed around the center.
- Since the angles between the lines connecting the center to each vertex are equal (72 degrees), the resultant force on the charge −Q will be zero.
- Thus, the assertion is true: the net electrostatic force on −Q is zero.
- The electrostatic potential V at a point due to a point charge is given by the formula:
\(
V = k \frac{q}{r}
\)
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point of interest.
- For the charge −Q at the center, the potential due to each +q charge is the same, and since there are five such charges, the total potential at the center is:
\(
V_{\text{total}} = 5 \cdot k \frac{q}{r}
\)
- This potential is non-zero because it is a scalar quantity and adds up.
- The assertion is true, but the reason is false. The net electrostatic potential at the center is not zero; it is a non-zero value due to the presence of the five positive charges.
- Assertion: True
- Reason: False
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Five equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionFive charges each q are placed at five corners regular pentagon. Distance from corner to the centre of pontagon is r. Then (K=14πε0)
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
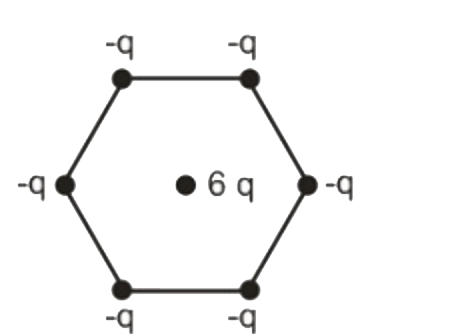
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
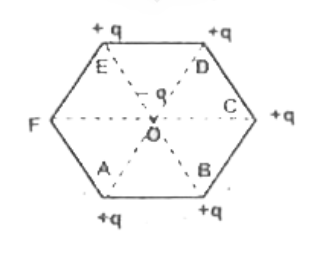
View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
View SolutionIf a charge q is placed at each vertex of a regular polygon, the net electric field at its centre is zero. Show it.
View SolutionA charge Q is place at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then Q/q equals:
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

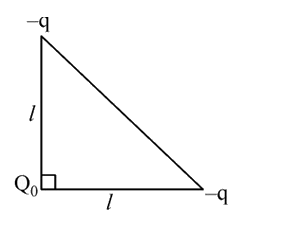
View SolutionThree charges Q0,−q and −q are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if Q 0 is equal to :
View Solution
