Assertion : Two concentric spherical shells A and B are charged by charges qA and qB. If qA is negative, then VA−VB is also negative.
Reason : VA−VB=(qA4πε0)(1RA−1rB)
therefore, if qA is negative, then VA−VB is also negative.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
To solve the problem, we need to analyze both the assertion and the reason given in the question.
Step 1: Understanding the Assertion
The assertion states that if two concentric spherical shells A and B are charged with charges qA and qB, and if qA is negative, then VA−VB is also negative.
Step 2: Understanding the Reason
The reason provided is the formula for the potential difference between the two shells:
VA−VB=(qA4πϵ0)(1RA−1RB)
This equation shows how the potential difference depends on the charges and the radii of the shells.
Step 3: Analyzing the Formula
1. Identify the terms:
- qA is the charge on shell A, which is given to be negative.
- RA and RB are the radii of shells A and B, respectively.
2. Substituting the charge:
Since qA is negative, the term qA4πϵ0 will also be negative.
3. Analyzing the expression:
- The term (1RA−1RB) will depend on the radii of the shells.
- If RA<RB, then 1RA>1RB, making the term positive.
- If RA>RB, then 1RA<1RB, making the term negative.
Step 4: Conclusion on VA−VB
- If RA<RB, VA−VB will be negative because a negative qA multiplied by a positive term results in a negative value.
- If RA>RB, VA−VB could be positive or negative depending on the magnitude of the terms.
Step 5: Final Evaluation
Since the assertion states that VA−VB is negative when qA is negative, and the reason correctly explains the relationship between the charges and the potential difference, we conclude that both the assertion and the reason are correct.
Final Answer
Both the assertion and the reason are correct.
---
The assertion states that if two concentric spherical shells A and B are charged with charges qA and qB, and if qA is negative, then VA−VB is also negative.
The reason provided is the formula for the potential difference between the two shells:
VA−VB=(qA4πϵ0)(1RA−1RB)
This equation shows how the potential difference depends on the charges and the radii of the shells.
1. Identify the terms:
- qA is the charge on shell A, which is given to be negative.
- RA and RB are the radii of shells A and B, respectively.
Since qA is negative, the term qA4πϵ0 will also be negative.
- The term (1RA−1RB) will depend on the radii of the shells.
- If RA<RB, then 1RA>1RB, making the term positive.
- If RA>RB, then 1RA<1RB, making the term negative.
- If RA<RB, VA−VB will be negative because a negative qA multiplied by a positive term results in a negative value.
- If RA>RB, VA−VB could be positive or negative depending on the magnitude of the terms.
Since the assertion states that VA−VB is negative when qA is negative, and the reason correctly explains the relationship between the charges and the potential difference, we conclude that both the assertion and the reason are correct.
Both the assertion and the reason are correct.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A and B are two concentric spherical shells. If A is given a charge +Q while B is earthed as shown in figure then
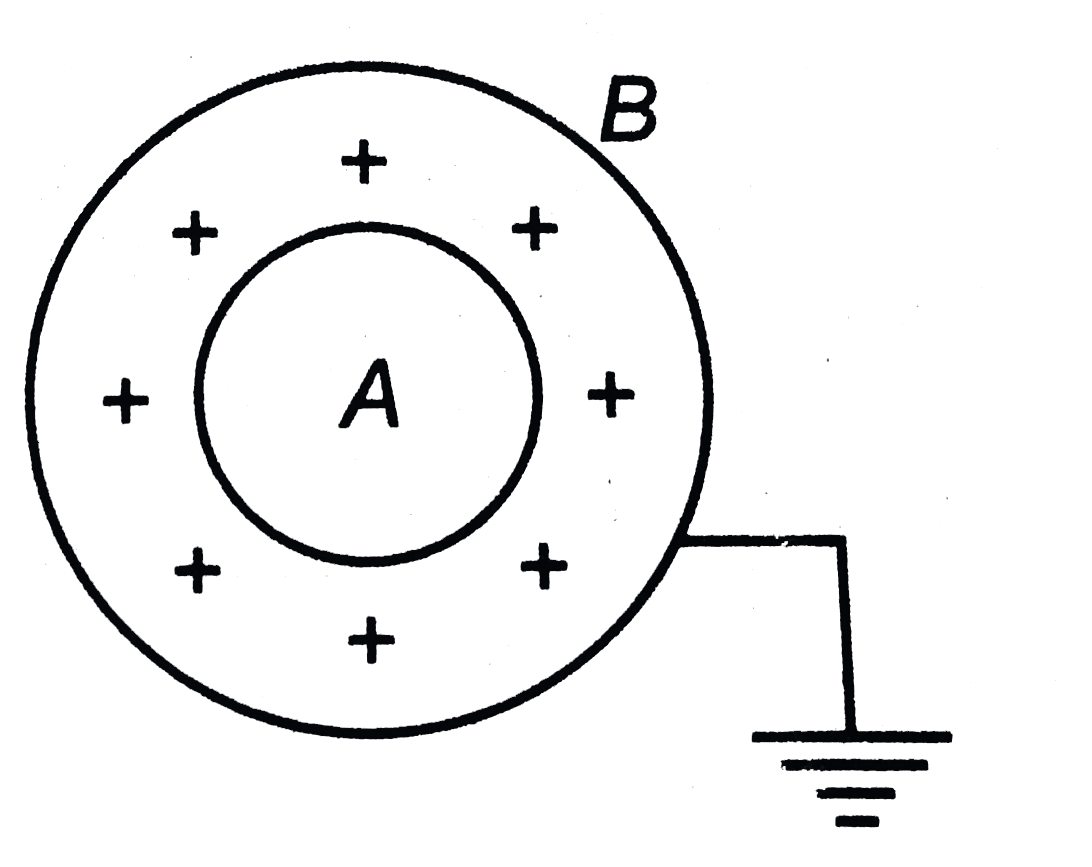
View SolutionA and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then

View SolutionTwo concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure

Choose the correct optin (K=14πε0)
View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b, and c. The shells A and C are given charge q and -q, respectively, and shell B is earthed. Then,
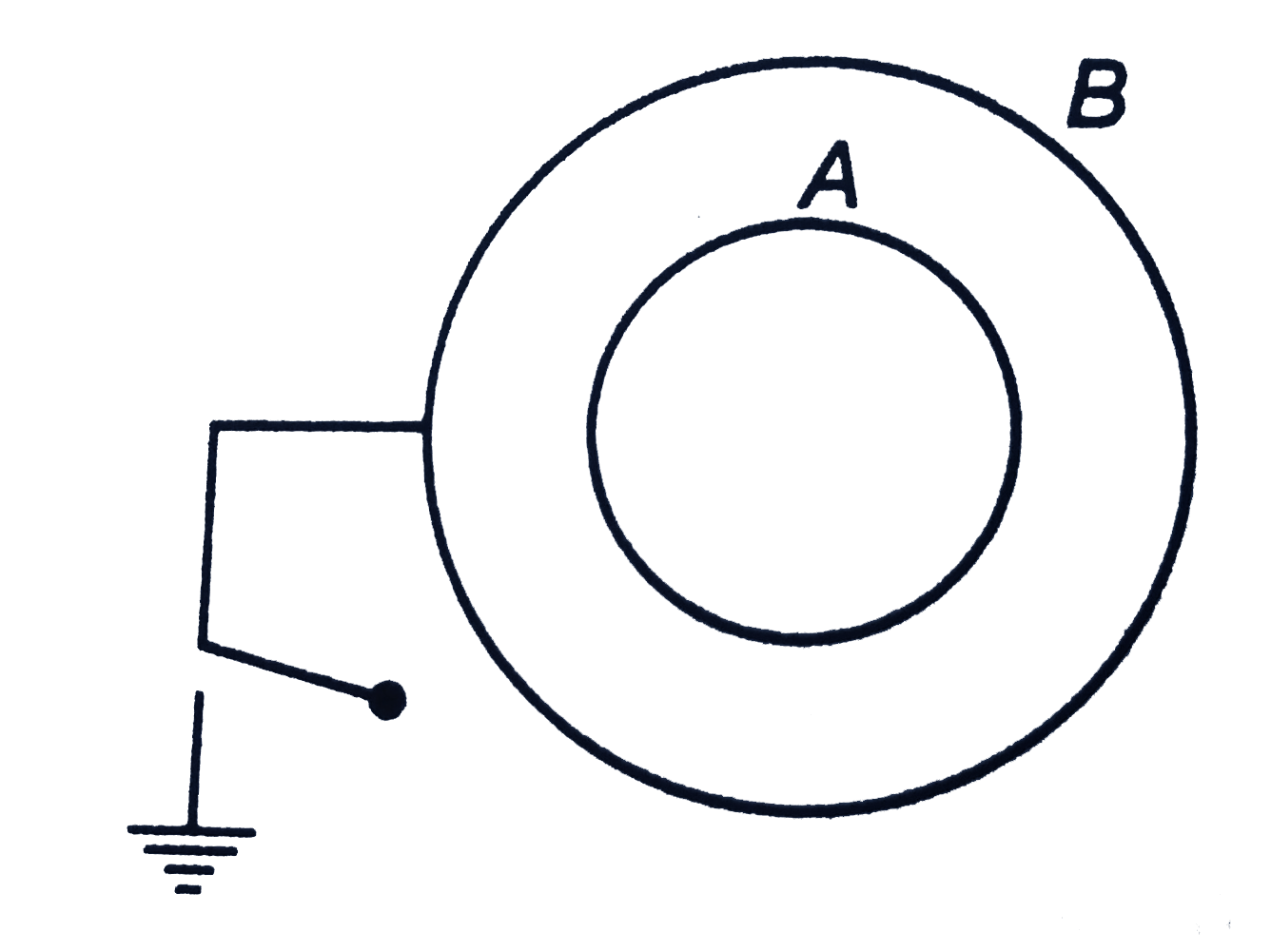
View SolutionTwo concentric shells have radii R and 2R charges qA and qB and potentials 2V and (32)V respectively. Now, shell B is earthed and let charges on them become qA' and qB'. Then,
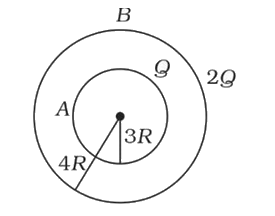
View SolutionIn the figure shown, conducting shells A and B have charges Q and 2Q distributed uniformly over and B. Value of VA−VB k is kQnR. Find n(k=14π∈0
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View Solution
