Assertion : A charged capacitor is disconnected from a battery. Now, if its plate are separated further, the potential energy will fall.
Reason : Energy stored in a capacitor is equal to the work done in charging it.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:D
To solve the problem, we need to analyze both the assertion and the reason given in the question.
Step 1: Understand the Assertion
The assertion states that when a charged capacitor is disconnected from a battery and its plates are separated further, the potential energy will fall.
- When a capacitor is charged and then disconnected from the battery, the charge Q on the capacitor remains constant.
- The capacitance C of a parallel plate capacitor is given by the formula:
C=Aϵ0d
where A is the area of the plates, ϵ0 is the permittivity of free space, and d is the separation between the plates.
Step 2: Analyze the Effect of Increasing Plate Separation
When the separation d is increased while the charge Q remains constant, the capacitance C decreases because C is inversely proportional to d.
- The potential energy U stored in a capacitor is given by:
U=Q22C
- As C decreases (due to increased d), the potential energy U actually increases because U is inversely related to C.
Conclusion for Assertion
Thus, the assertion that the potential energy will fall is false.
Step 3: Understand the Reason
The reason states that the energy stored in a capacitor is equal to the work done in charging it.
- The work done W in charging a capacitor can be expressed as:
W=∫Q0VdQ
where V is the voltage across the capacitor.
- Since V=QC, we can substitute this into the integral to find that the work done in charging the capacitor is indeed equal to the energy stored in it.
Conclusion for Reason
The reason is true because the energy stored in a capacitor is equal to the work done in charging it.
Final Conclusion
Since the assertion is false and the reason is true, the correct answer is that the assertion is false while the reason is true.
Summary of Steps
1. Analyze the assertion about potential energy when the capacitor is disconnected and plates are separated.
2. Understand the relationship between capacitance, charge, and potential energy.
3. Evaluate the reason regarding the work done in charging the capacitor.
4. Conclude that the assertion is false and the reason is true.
The assertion states that when a charged capacitor is disconnected from a battery and its plates are separated further, the potential energy will fall.
- The capacitance C of a parallel plate capacitor is given by the formula:
C=Aϵ0d
where A is the area of the plates, ϵ0 is the permittivity of free space, and d is the separation between the plates.
When the separation d is increased while the charge Q remains constant, the capacitance C decreases because C is inversely proportional to d.
U=Q22C
- As C decreases (due to increased d), the potential energy U actually increases because U is inversely related to C.
Thus, the assertion that the potential energy will fall is false.
The reason states that the energy stored in a capacitor is equal to the work done in charging it.
W=∫Q0VdQ
where V is the voltage across the capacitor.
- Since V=QC, we can substitute this into the integral to find that the work done in charging the capacitor is indeed equal to the energy stored in it.
The reason is true because the energy stored in a capacitor is equal to the work done in charging it.
Since the assertion is false and the reason is true, the correct answer is that the assertion is false while the reason is true.
1. Analyze the assertion about potential energy when the capacitor is disconnected and plates are separated.
2. Understand the relationship between capacitance, charge, and potential energy.
3. Evaluate the reason regarding the work done in charging the capacitor.
4. Conclude that the assertion is false and the reason is true.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionThree initially uncharged capacitors are connected to a battery of 10V is parallel combination find out following
(i) charge flow from the battery
(ii) total energy stored in the capacitors
(iii) heat produced in the circuit
(iv) potential energy in the 3μF capacitor.
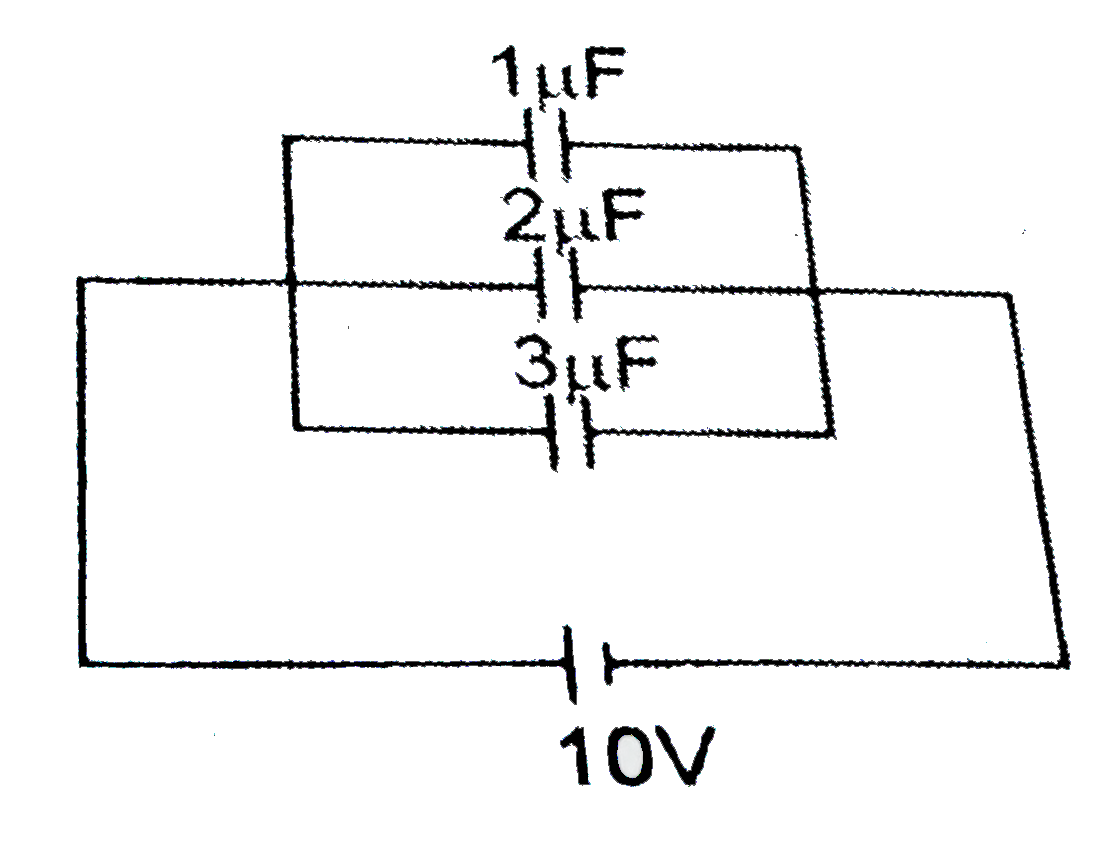
View Solution
Knowledge Check
Energies stored in capacitor and dissipated during charging a capacitor bear a ratio
A1:1B1:2C2:1D1:3
An uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is
View SolutionAssertion : When an uncharged capacitor is charged by a battery only 50% of the energy supplied is stored in the capacitor.
Reason : Rest 50% is lost.
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionAssertion : When a capacitor is charged by a battery. Half of the energy supplied by the battery is stored in the capacitor and rest half is lost.
Reason : If resistance in the circuit is zero, then there will be no loss of energy.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA parallel plate vacuum capacitor with plate area A and separation x has charges +Q and −Q on its plates. The capacitor is disconnected from the source of charge, so the charge on each plate remains fixed.
(a) What is the total energy stored in the capacitor?
(b) The plates are pulled apart an additional distance dx. What is the change in the stored energy?
(c) If F is the force with which the plates attract each other, then the change in the stored energy must equal the work dW=Fdx done in pulling the plates apart. Find an expression for F.
(d) Explain why F is not equal to QE, where E is the electric field between the plates.
View SolutionA parallel plate vacuum capacitor eith plate area A and separation x has charges+Q and −Q on its plates. The capacitor is disconnected from the source of charge, so the charge on each plate remains fixed.
a. What is the total energy stored in the capacitor?
b. The plates are pulled apart an additional distance each case.
c. If F is the force with which the plates attract each other, the change in the stored energy must equal the work dW=Fdx done in pulling the plates apart. Find an expression for F
d. Energy storage in a capacitor can be limited by the maximum electric field between the plates. What is the ratio of the electric field for the series for parallel combinations?
View Solution
