Two charges of equal magnitude q are placed in air at a distance 2a apart and third charge −2q is placed at mid-point . The potential energy of the system is (ε0 = permittivity of free space)
−q28πε0a
−3q28πε0a
−5q28πε0a
−7q28πε0a
The correct Answer is:D
To find the potential energy of the system of three charges, we can follow these steps:
Step 1: Identify the Charges and Their Positions
We have two charges q located at points A and B, and a charge −2q located at the midpoint C between A and B. The distance between A and B is 2a, so the distances from A to C and B to C are both a.
Step 2: Write the Formula for Potential Energy
The potential energy U of a system of point charges is given by the formula:
U=k∑qiqjrij
where k is Coulomb's constant, qi and qj are the point charges, and rij is the distance between them.
Step 3: Calculate the Potential Energy Contributions
We will calculate the potential energy contributions from each pair of charges:
1. Between charges at A and B:
UAB=kq⋅q2a=kq22a
2. Between charges at A and C:
UAC=kq⋅(−2q)a=−2kq2a
3. Between charges at B and C:
UBC=k(−2q)⋅qa=−2kq2a
Step 4: Sum the Potential Energies
Now, we sum the contributions from all pairs:
U=UAB+UAC+UBC
Substituting the values we calculated:
U=kq22a−2kq2a−2kq2a
U=kq22a−4kq2a
To combine these, we can express −4kq2a as −8kq22a:
U=kq22a−8kq22a=−7kq22a
Step 5: Substitute the Value of k
Recall that Coulomb's constant k can be expressed as:
k=14πϵ0
Substituting this into our equation gives:
U=−7(14πϵ0)q22a
This simplifies to:
U=−7q28πϵ0a
Final Answer
Thus, the potential energy of the system is:
U=−7q28ϵ0a
---
We have two charges q located at points A and B, and a charge −2q located at the midpoint C between A and B. The distance between A and B is 2a, so the distances from A to C and B to C are both a.
The potential energy U of a system of point charges is given by the formula:
U=k∑qiqjrij
where k is Coulomb's constant, qi and qj are the point charges, and rij is the distance between them.
We will calculate the potential energy contributions from each pair of charges:
UAB=kq⋅q2a=kq22a
UAC=kq⋅(−2q)a=−2kq2a
UBC=k(−2q)⋅qa=−2kq2a
Now, we sum the contributions from all pairs:
U=UAB+UAC+UBC
Substituting the values we calculated:
U=kq22a−2kq2a−2kq2a
U=kq22a−4kq2a
To combine these, we can express −4kq2a as −8kq22a:
U=kq22a−8kq22a=−7kq22a
Recall that Coulomb's constant k can be expressed as:
k=14πϵ0
Substituting this into our equation gives:
U=−7(14πϵ0)q22a
This simplifies to:
U=−7q28πϵ0a
Thus, the potential energy of the system is:
U=−7q28ϵ0a
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo positive point charges of unequal magnitude are placed at a certain distance apart. A small positive test charge is placed at null point, then
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
View SolutionTwo charges q and -3q are placed fixed on x-axis separated by distance d. where should a third charge 2q be placed such that it will not experience any force?
View SolutionTwo charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo free point charges +qand+4q are placed apart a distance x. A third charge is so placed that all the three charges are in equilibrium. Then
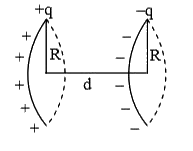
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View Solution
