In a metre bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
The correct Answer is:40cm
To solve the problem of finding the balance point on a metre bridge when two resistances are in the ratio of 2:3, we can follow these steps:
1. Understanding the Problem:
We have a metre bridge (100 cm long) and two resistances P and Q in the ratio 2:3. We need to find the position (length from one end) where the bridge balances.
2. Assigning Values:
Let the resistance P be 2x and the resistance Q be 3x, where x is a common factor.
3. Using the Balance Condition:
According to the principle of the metre bridge, the ratio of the lengths on either side of the bridge is equal to the ratio of the resistances:
PQ=L1L2
where L1 is the length from one end to the balance point, and L2 is the remaining length. Since the total length of the wire is 100 cm, we have:
L2=100−L1
4. Setting Up the Equation:
Substituting the values of P and Q into the ratio gives:
2x3x=L1100−L1
Simplifying this, we get:
23=L1100−L1
5. Cross-Multiplying:
Cross-multiplying to eliminate the fraction:
2(100−L1)=3L1
Expanding this, we have:
200−2L1=3L1
6. Rearranging the Equation:
Bringing all terms involving L1 to one side:
200=3L1+2L1
This simplifies to:
200=5L1
7. Solving for L1:
Dividing both sides by 5 gives:
L1=2005=40 cm
8. Conclusion:
Therefore, the balance point will be obtained at a length of 40 cm from one end of the metre bridge.
Final Answer:
The balance point will be at 40 cm.
---
We have a metre bridge (100 cm long) and two resistances P and Q in the ratio 2:3. We need to find the position (length from one end) where the bridge balances.
Let the resistance P be 2x and the resistance Q be 3x, where x is a common factor.
According to the principle of the metre bridge, the ratio of the lengths on either side of the bridge is equal to the ratio of the resistances:
PQ=L1L2
where L1 is the length from one end to the balance point, and L2 is the remaining length. Since the total length of the wire is 100 cm, we have:
L2=100−L1
Substituting the values of P and Q into the ratio gives:
2x3x=L1100−L1
Simplifying this, we get:
23=L1100−L1
Cross-multiplying to eliminate the fraction:
2(100−L1)=3L1
Expanding this, we have:
200−2L1=3L1
Bringing all terms involving L1 to one side:
200=3L1+2L1
This simplifies to:
200=5L1
Dividing both sides by 5 gives:
L1=2005=40 cm
Therefore, the balance point will be obtained at a length of 40 cm from one end of the metre bridge.
The balance point will be at 40 cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-6
5 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-3
4 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections,the unknown resistance is
View SolutionA resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm and an unknown resistance, greater than 2Ω, is connected across the other gap. When these resistance are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is.
(a)3Ω
(b) 4Ω
( c) 5Ω
(d) 6Ω.
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
In a metre bridge, the gaps are closed by two resistance P and Q and the balance point is obtained at 40cm. When Q is shunted by a resistance of 10Ω, the balance point shifts to 50cm. The values of P and Q are.
 .
.
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
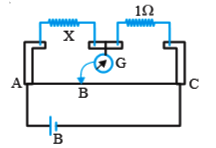
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View Solution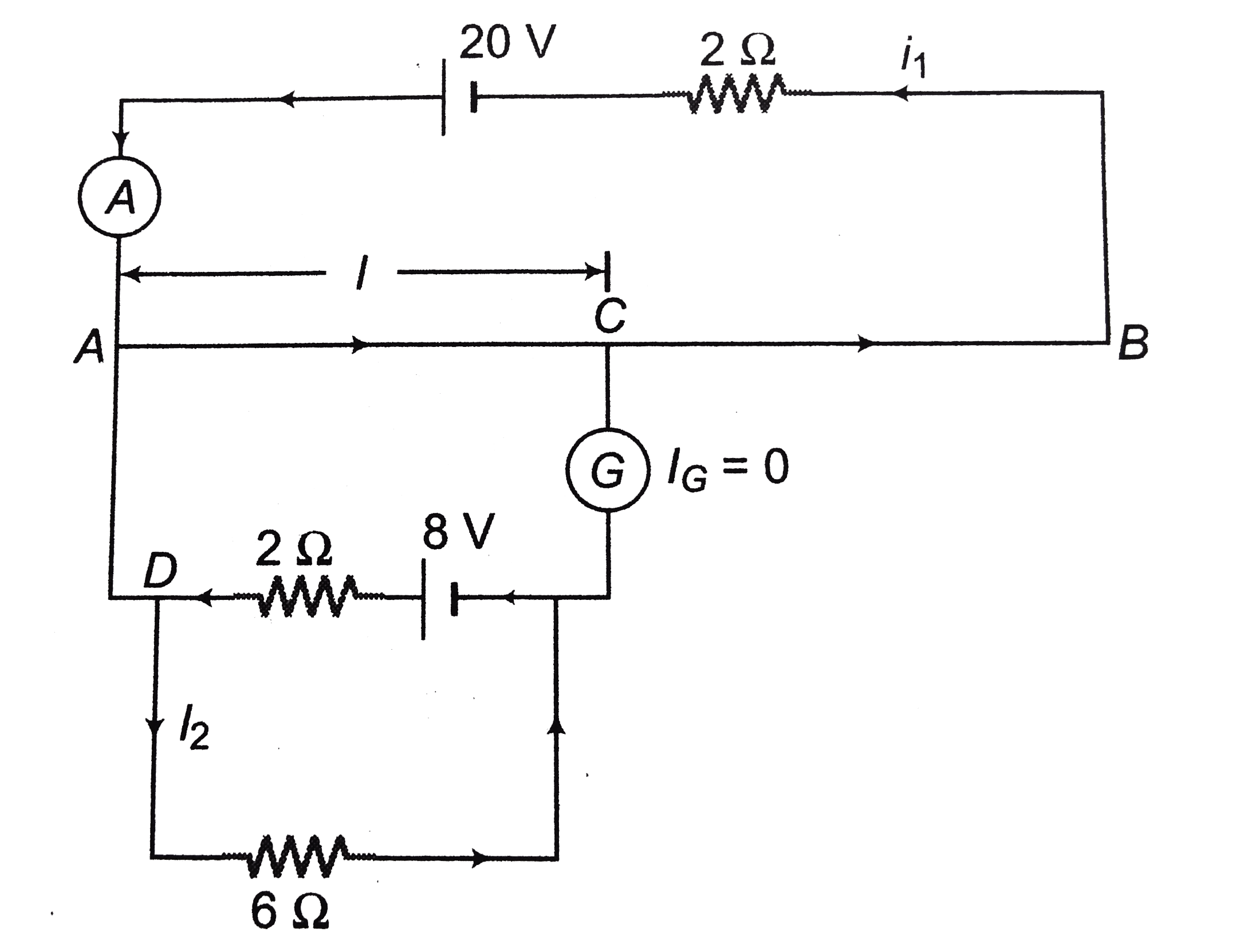
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
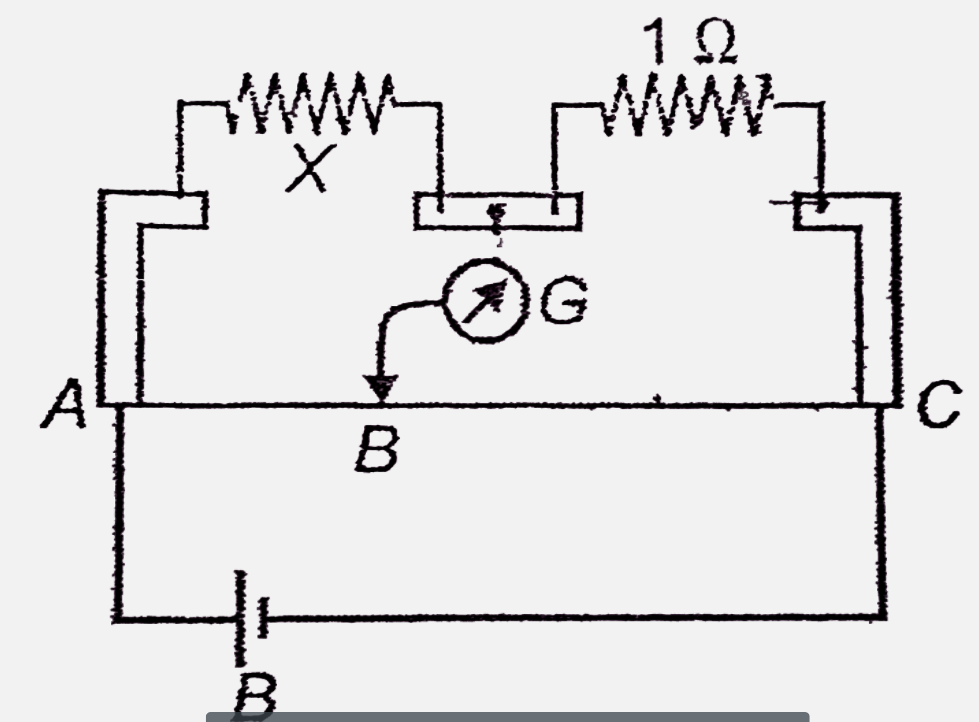
View SolutionFigure shows a metre bridge in which a known resistance R and an unknown resistance X connected to it. The length of the total wire AB is 100cm. Then the balancing length for which the percentage error in measuring the value of x is minimum (neglect end corrections)
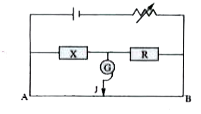
View Solution
