The resistance of a bulb filamanet is 100Ω at a temperature of 100∘C. If its temperature coefficient of resistance be 0.005per.∘C, its resistance will become 200Ω at a temperature of
500∘C
300∘C
200∘C
400∘C
The correct Answer is:B
To solve the problem, we need to find the temperature at which the resistance of a bulb filament becomes 200 ohms, given its initial resistance and temperature, as well as its temperature coefficient of resistance.
1. Identify Given Values:
- Initial resistance R1=100Ω at temperature T1=100∘C
- Final resistance R2=200Ω
- Temperature coefficient of resistance α=0.005per∘C
2. Use the Resistance Temperature Formula:
The resistance of a conductor at a temperature T can be expressed as:
R=R0(1+α(T−T0))
where R0 is the resistance at temperature T0.
3. Set Up the Equations:
For the initial condition:
R1=R0(1+α(T1−T0))
Substituting the known values:
100=R0(1+0.005×(100−T0))
For the final condition:
R2=R0(1+α(T2−T0))
Substituting the known values:
200=R0(1+0.005×(T2−T0))
4. Divide the Two Equations:
Dividing the second equation by the first:
200100=R0(1+0.005(T2−T0))R0(1+0.005(100−T0))
This simplifies to:
2=1+0.005(T2−T0)1+0.005(100−T0)
5. Cross Multiply and Simplify:
Cross multiplying gives:
2(1+0.005(100−T0))=1+0.005(T2−T0)
Expanding both sides:
2+1−0.01T0=0.005T2−0.005T0
Rearranging gives:
1=0.005T2−0.005T0−0.01T0
1=0.005T2−0.015T0
6. Solve for T2:
Rearranging for T2:
0.005T2=1+0.015T0
T2=1+0.015T00.005
Substituting T0=100:
T2=1+0.015×1000.005=1+1.50.005=2.50.005=500
7. Final Answer:
Therefore, the temperature at which the resistance becomes 200 ohms is:
T2=400∘C
- Initial resistance R1=100Ω at temperature T1=100∘C
- Final resistance R2=200Ω
- Temperature coefficient of resistance α=0.005per∘C
The resistance of a conductor at a temperature T can be expressed as:
R=R0(1+α(T−T0))
where R0 is the resistance at temperature T0.
For the initial condition:
R1=R0(1+α(T1−T0))
Substituting the known values:
100=R0(1+0.005×(100−T0))
For the final condition:
R2=R0(1+α(T2−T0))
Substituting the known values:
200=R0(1+0.005×(T2−T0))
Dividing the second equation by the first:
200100=R0(1+0.005(T2−T0))R0(1+0.005(100−T0))
This simplifies to:
2=1+0.005(T2−T0)1+0.005(100−T0)
Cross multiplying gives:
2(1+0.005(100−T0))=1+0.005(T2−T0)
Expanding both sides:
2+1−0.01T0=0.005T2−0.005T0
Rearranging gives:
1=0.005T2−0.005T0−0.01T0
1=0.005T2−0.015T0
Rearranging for T2:
0.005T2=1+0.015T0
T2=1+0.015T00.005
Substituting T0=100:
T2=1+0.015×1000.005=1+1.50.005=2.50.005=500
Therefore, the temperature at which the resistance becomes 200 ohms is:
T2=400∘C
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
If the resistance of a conductor is 5Ω at 50∘C and 7Ω at 100∘C then the mean temperature coefficient of resistance of the material is
View SolutionDefine temperature coefficient of resistance of the material of a conductor.
View SolutionA comon flashlight bulb is rated 0.30A and 2.7V (the values of the current and voltage under operating conditions.) If the resistance of the tungsten bulb filament at room temperature 20∘C is 1.0Ω and its temperature coefficient of resistivity is 4.0×10−3C−1, then find the temperature in centigrade of the filament when the bulb is on. (Consider the variationi of resistance to be linear with temperature.)
View SolutionA metallic wire has a resistance of 3.0Ω at 0∘C and 4.8Ω at 150∘C. Find the temperature coefficient of resistance of its material.
View SolutionThe resistance of a wire at 20∘C is 20Ω and at 500∘C is 60Ω. At which temperature its resistance will be 25Ω?
View SolutionA copper coil has resistance of 20.0Ωat0∘C and a resistance of 26.4Ωat80∘C. Find the temperature coefficient of resistance of copper.
View SolutionTwo coils connected in series have resistance of 600KΩ and 300Ω at 20∘C and temperature coefficient of0.001 and 0.004(.∘C)−1 respectively. Find resistance of the combination at a temperature of 50∘C. What is the effective temperature coefficient of combination?
View SolutionVariation of resistance of the conductor with temperature is shown . Temperature coefficient of the conductor is
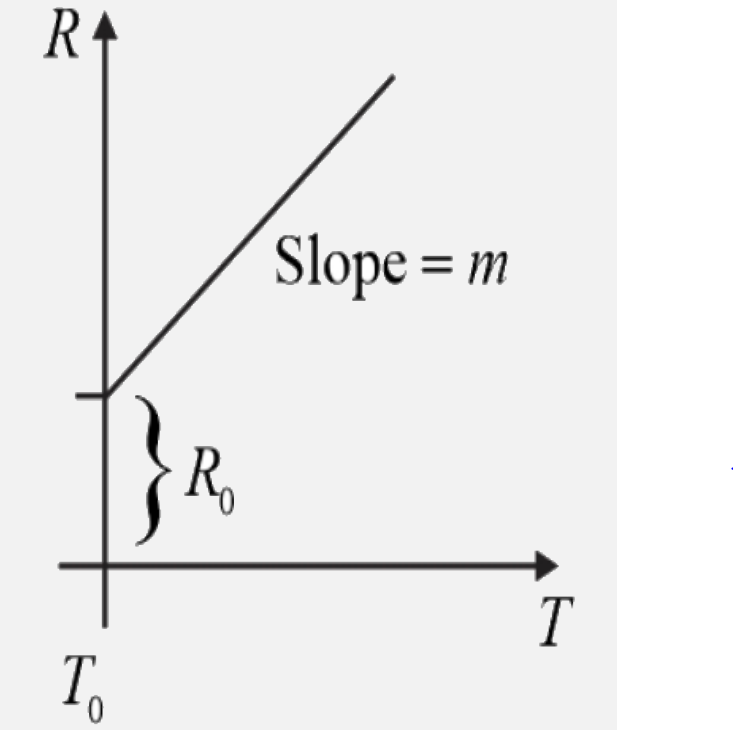
View SolutionThe resistance of a conductor is 5Ω at 50∘C and 6Ω at 100∘C. The resistance at 0∘C is
View SolutionThe temperature coefficient of resistance of a wire is 0.00145∘C−1. At 100∘C its resistance is 2Ω. At what temperature the resistance of the wire be 3Ω?
View Solution
