A galvanometer having resistance of 50Ω requires a current of 100ΩA to given full scale deflection. How much resistance is required to convert it into an ammeter of range of 10 A ?
5×10−3Ω in series
5×10−4Ω in parallel
105Ω in series
105Ω in parallel
The correct Answer is:B
To solve the problem of converting a galvanometer into an ammeter with a specific range, we can follow these steps:
Step 1: Understand the given values
- Resistance of the galvanometer (G) = 50 Ω
- Full-scale deflection current (Ig) = 100 µA = 100 × 10^(-6) A
- Desired range of the ammeter (I) = 10 A
Step 2: Calculate the current through the shunt resistor
The current flowing through the galvanometer is 100 µA, and the total current through the ammeter will be 10 A. Therefore, the current flowing through the shunt resistor (R) can be calculated as:
IR=I−Ig=10A−100µA=10A−0.0001A=9.9999A
For practical purposes, we can approximate this to:
IR≈10A
Step 3: Apply the principle of parallel resistances
Since the galvanometer and the shunt resistor are in parallel, the voltage across both must be the same. The voltage across the galvanometer can be expressed as:
Vg=Ig⋅G=(100×10−6)⋅50
Calculating this gives:
Vg=0.005V=5mV
Step 4: Set up the equation for the shunt resistor
The voltage across the shunt resistor (R) is also equal to the voltage across the galvanometer:
VR=IR⋅R
Setting the voltages equal gives:
Ig⋅G=IR⋅R
Substituting the values we have:
(100×10−6)⋅50=9.9999⋅R
Step 5: Solve for R
Now we can solve for R:
R=(100×10−6)⋅509.9999
Calculating the numerator:
(100×10−6)⋅50=0.005
So,
R=0.0059.9999≈0.0005Ω
or
R=5×10−4Ω
Step 6: Conclusion
The resistance required to convert the galvanometer into an ammeter of range 10 A is approximately:
R≈5×10−4Ω
- Resistance of the galvanometer (G) = 50 Ω
- Full-scale deflection current (Ig) = 100 µA = 100 × 10^(-6) A
- Desired range of the ammeter (I) = 10 A
The current flowing through the galvanometer is 100 µA, and the total current through the ammeter will be 10 A. Therefore, the current flowing through the shunt resistor (R) can be calculated as:
IR=I−Ig=10A−100µA=10A−0.0001A=9.9999A
For practical purposes, we can approximate this to:
IR≈10A
Since the galvanometer and the shunt resistor are in parallel, the voltage across both must be the same. The voltage across the galvanometer can be expressed as:
Vg=Ig⋅G=(100×10−6)⋅50
Vg=0.005V=5mV
The voltage across the shunt resistor (R) is also equal to the voltage across the galvanometer:
VR=IR⋅R
Setting the voltages equal gives:
Ig⋅G=IR⋅R
Substituting the values we have:
(100×10−6)⋅50=9.9999⋅R
Now we can solve for R:
R=(100×10−6)⋅509.9999
Calculating the numerator:
(100×10−6)⋅50=0.005
So,
R=0.0059.9999≈0.0005Ω
or
R=5×10−4Ω
The resistance required to convert the galvanometer into an ammeter of range 10 A is approximately:
R≈5×10−4Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A galvanometer coil has a resistance of 990Ω and it shows full scale deflection for a current of 10mA. Calculate the value of resistance required to convert it into an ammeter of range 1 A.
View SolutionA galvenometer has a resistance of 30Ω, and a current of 2mA is needed for a full- scale deflection. What is the resistance and how is it to be connected to converted to the voltmeter of 0−2V range?
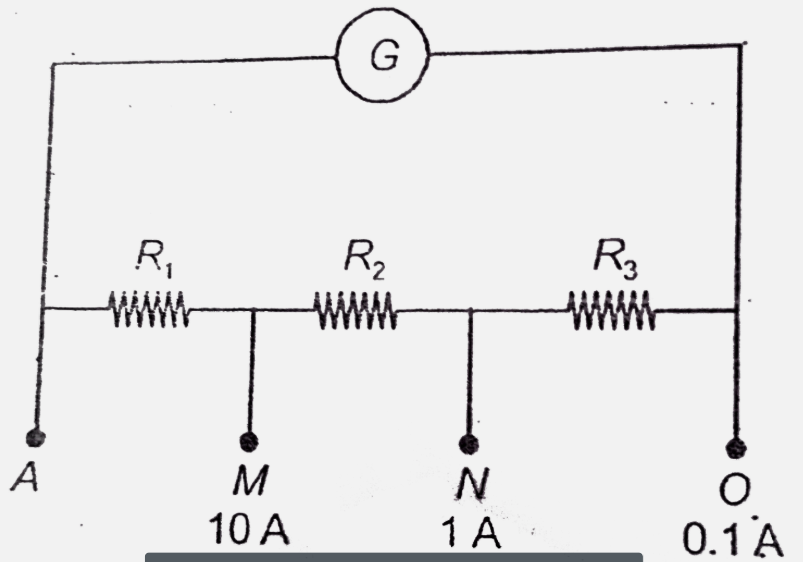
View SolutionThe galvanometer shown in figure has resistance 50 Ω and current required for full scale deflection is 1mA. Find the resistance R1,R2 and required to convert to convert it into ammeter having ranges as indicated.
View SolutionA galvanometer has a resistance of 30 ohm and a current of 2 mA is needed to give a full scale deflection. What is the resistance needed and how is it to be connected to convert this galvanometer
(a) Into an ammeter of 0.3 A range ?
(b) Into a volmeter of 0.2 V range ?
View SolutionThe resistance of a moving coil galvanometer is 20Ω. It requires 0.01 A current for full - scale deflection. The value of resistance to convert it into a voltmeter of the range 20 V will be
View SolutionA micrometer has a resistance of 100Ω and full scale deflection current of 50μA. How can it be made to work as an ammeter of range 5mA?
View SolutionThe resistance of a galvanometer coil is R. What is the shunt resistance required to convert it into an ammeter of range 4 times
View Solution(a) Briefly explain how a galvanometer is converted into an ammeter.
(b) A galvanometer coil has a resistance of 15Ω and it shows full scale deflection for a current of 4 mA. Convert it into an ammeter of range 0 to 6 A.
View SolutionA galvanometer of resistance 100Ω gives full deffection for a current 10−5 the value of shunt required to convert it into ammeter of range 1 ampere is:-
View SolutionA galvanometer with its coil resistance 25Ω requires a current of 1 mA for its full deflection. In order to construct an ammeter to read up to a current of 2A, the approximate value of the shunt resistance should be :
View Solution
