6Ω and 12Ω resistors are connected in parallel. This combination is connected in series with 10 V battery and 6Ω resistor. What is the potential differnce between the terminals of the 12Ω resistor ?
4 V
16 V
2
8 V
The correct Answer is:A
To solve the problem step by step, we will follow the outlined process in the video transcript and add some explanations along the way.
Step 1: Understand the Circuit Configuration
We have a 6Ω resistor and a 12Ω resistor connected in parallel. This parallel combination is connected in series with a 6Ω resistor and a 10V battery.
Step 2: Draw the Circuit
The circuit can be represented as follows:
- Connect the 10V battery to a 6Ω resistor (let's call this R1).
- From the other end of R1, connect the parallel combination of the 6Ω (let's call this R2) and 12Ω (let's call this R3) resistors.
Step 3: Calculate the Equivalent Resistance of the Parallel Combination
The equivalent resistance \( R_{XY} \) of the 6Ω and 12Ω resistors in parallel can be calculated using the formula:
\(
\frac{1}{R_{XY}} = \frac{1}{R_2} + \frac{1}{R_3}
\)
Substituting the values:
\(
\frac{1}{R_{XY}} = \frac{1}{6} + \frac{1}{12}
\)
Finding a common denominator (which is 12):
\(
\frac{1}{R_{XY}} = \frac{2}{12} + \frac{1}{12} = \frac{3}{12} = \frac{1}{4}
\)
Thus, the equivalent resistance \( R_{XY} \) is:
\(
R_{XY} = 4Ω
\)
Step 4: Calculate the Total Resistance in the Circuit
The total resistance \( R_{total} \) in the circuit is the sum of the series resistances:
\(
R_{total} = R_1 + R_{XY} = 6Ω + 4Ω = 10Ω
\)
Step 5: Calculate the Total Current in the Circuit
Using Ohm's Law, the current \( I \) in the circuit can be calculated as:
\(
I = \frac{V}{R_{total}} = \frac{10V}{10Ω} = 1A
\)
Step 6: Calculate the Voltage Across the Parallel Combination
The voltage across the parallel combination (which is also the voltage across the 6Ω and 12Ω resistors) can be calculated using Ohm's Law:
\(
V_{XY} = I \times R_{XY} = 1A \times 4Ω = 4V
\)
Step 7: Conclusion
Thus, the potential difference between the terminals of the 12Ω resistor is 4V.
---
We have a 6Ω resistor and a 12Ω resistor connected in parallel. This parallel combination is connected in series with a 6Ω resistor and a 10V battery.
The circuit can be represented as follows:
- Connect the 10V battery to a 6Ω resistor (let's call this R1).
- From the other end of R1, connect the parallel combination of the 6Ω (let's call this R2) and 12Ω (let's call this R3) resistors.
The equivalent resistance \( R_{XY} \) of the 6Ω and 12Ω resistors in parallel can be calculated using the formula:
\(
\frac{1}{R_{XY}} = \frac{1}{R_2} + \frac{1}{R_3}
\)
Substituting the values:
\(
\frac{1}{R_{XY}} = \frac{1}{6} + \frac{1}{12}
\)
Finding a common denominator (which is 12):
\(
\frac{1}{R_{XY}} = \frac{2}{12} + \frac{1}{12} = \frac{3}{12} = \frac{1}{4}
\)
Thus, the equivalent resistance \( R_{XY} \) is:
\(
R_{XY} = 4Ω
\)
The total resistance \( R_{total} \) in the circuit is the sum of the series resistances:
\(
R_{total} = R_1 + R_{XY} = 6Ω + 4Ω = 10Ω
\)
Using Ohm's Law, the current \( I \) in the circuit can be calculated as:
\(
I = \frac{V}{R_{total}} = \frac{10V}{10Ω} = 1A
\)
The voltage across the parallel combination (which is also the voltage across the 6Ω and 12Ω resistors) can be calculated using Ohm's Law:
\(
V_{XY} = I \times R_{XY} = 1A \times 4Ω = 4V
\)
Thus, the potential difference between the terminals of the 12Ω resistor is 4V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Two resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power dissipated in each resistor.
View Solution50Ω and 100Ω resistors are connected in series. This connection is connected with a battery of 2.4 volts. When a voltmeter of 100Ω resistance is connected across 100Ω resistor, then the reading of the voltmeter will be
View Solution
Knowledge Check
Three resistors 2Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 20V and negligible internal Resistance. The total current drawn from the battery is
A10AB15AC19AD23A
If power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
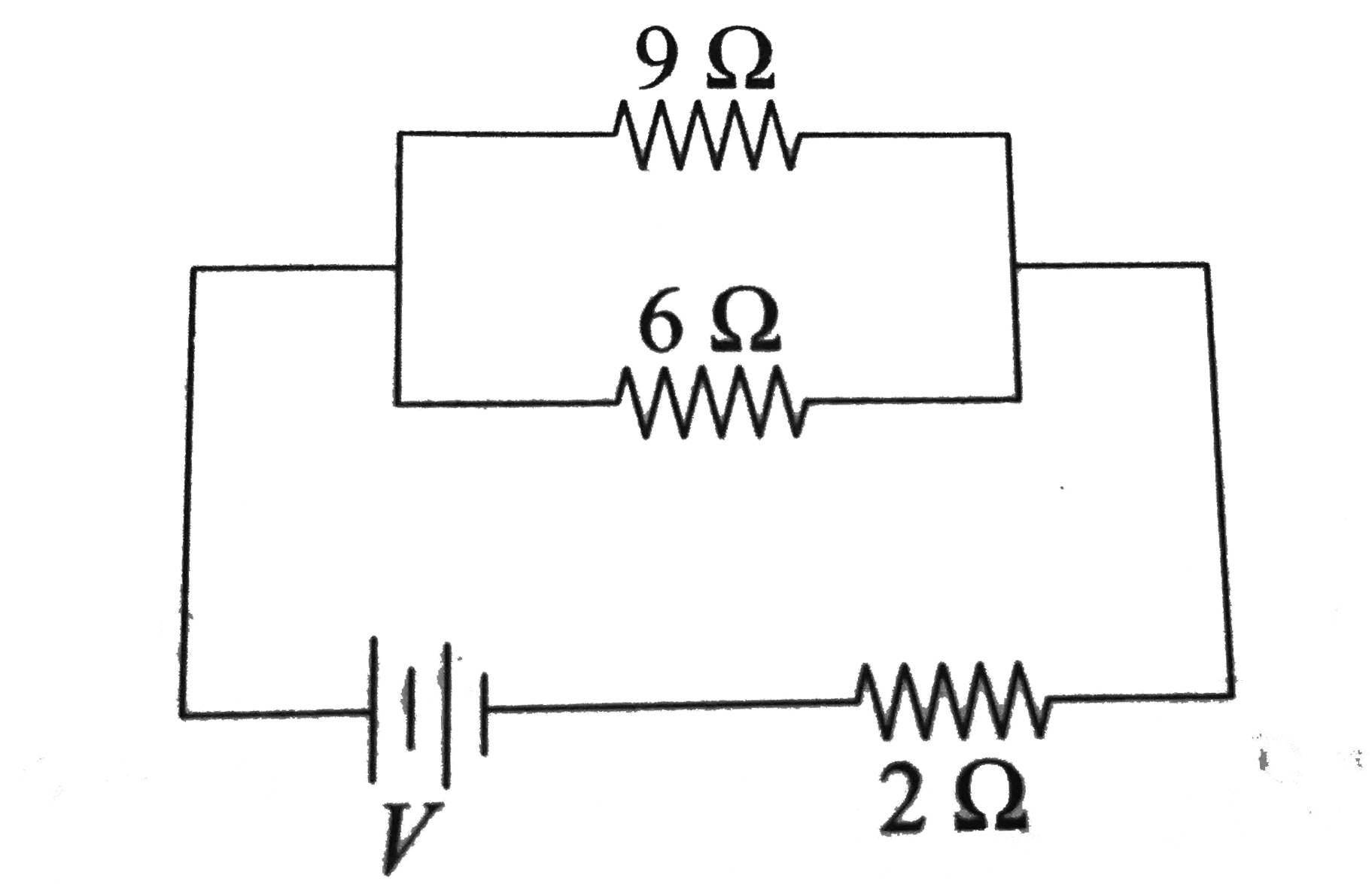
View SolutionThree resistors are connected to a 12 V battery as shown in the figure given below :
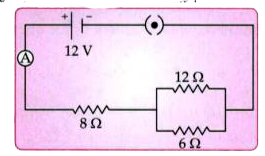
What is the potential difference across the parallel combination of 6 ohm and 12 ohm resistor ?
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate :the current through each resistor
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate :the current through the battery
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate : (a) the total resistance of the circuit,
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View Solution
