Magnetic field due to a ring having n turns at a distance x on its axis is proportional to (if r= radius of ring)
(a) r(x2+r2)
(b) r(x2+r2)3/2
(c) nr2(x2+r2)3/2
(d) n2r2(x2+r2)3/2
The correct Answer is:C
To find the magnetic field due to a ring with n turns at a distance x on its axis, we can follow these steps:
1. Understand the Setup:
- We have a circular ring of radius r carrying a current I.
- We want to find the magnetic field at a point P located at a distance x along the axis of the ring.
2. Use Biot-Savart Law:
- According to the Biot-Savart Law, the magnetic field dB due to a small current element dL is given by:
dB=μ04πIdLsinθr2
- Here, θ is the angle between the current element and the line connecting the element to the point P.
3. Determine sinθ:
- In the right triangle formed by the radius r, the distance x, and the distance from the current element to point P:
sinθ=r√x2+r2
4. Substituting sinθ into dB:
- Substitute sinθ into the expression for dB:
dB=μ04πIdL⋅r√x2+r2(x2+r2)
5. Integrate Over the Ring:
- The total magnetic field B is obtained by integrating dB around the entire ring:
B=∫dB=∫μ0Ir4πdL(x2+r2)3/2
- The integral of dL around the ring is 2πr:
B=μ0Ir4π⋅2πr(x2+r2)3/2=μ0Ir22(x2+r2)3/2
6. Considering n Turns:
- For n turns, the magnetic field becomes:
B=μ0nIr22(x2+r2)3/2
7. Identify Proportionality:
- From the final expression, we can see that the magnetic field B is proportional to:
B∝r2(x2+r2)3/2
Final Answer:
The magnetic field due to a ring having n turns at a distance x on its axis is proportional to:
r2(x2+r2)3/2
- We have a circular ring of radius r carrying a current I.
- We want to find the magnetic field at a point P located at a distance x along the axis of the ring.
- According to the Biot-Savart Law, the magnetic field dB due to a small current element dL is given by:
dB=μ04πIdLsinθr2
- Here, θ is the angle between the current element and the line connecting the element to the point P.
- In the right triangle formed by the radius r, the distance x, and the distance from the current element to point P:
sinθ=r√x2+r2
- Substitute sinθ into the expression for dB:
dB=μ04πIdL⋅r√x2+r2(x2+r2)
- The total magnetic field B is obtained by integrating dB around the entire ring:
B=∫dB=∫μ0Ir4πdL(x2+r2)3/2
- The integral of dL around the ring is 2πr:
B=μ0Ir4π⋅2πr(x2+r2)3/2=μ0Ir22(x2+r2)3/2
- For n turns, the magnetic field becomes:
B=μ0nIr22(x2+r2)3/2
- From the final expression, we can see that the magnetic field B is proportional to:
B∝r2(x2+r2)3/2
The magnetic field due to a ring having n turns at a distance x on its axis is proportional to:
r2(x2+r2)3/2
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
The field due to a magnet at a distance R~ from the centre of the magnet is proportional
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA uniformly charged ring of radius R is rotated about its axis with constant linear speed v of each of its particle. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from centre of ring is (c is speed of light )

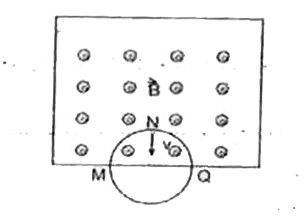
View SolutionA thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
View SolutionA charge -q is placed at the axis of a charged ring of radius at a distance of 2√2 r as show in figure . If ring is fixed and carrying charge Q, the kinetic energy of charge - q when it is relased and reaches the centre of ring will be qQnπε0r.Find n

View SolutionThere is a conducting ring of radius R. Another ring having current i and radius r(r<<R) is kept on the axis of bigger ring such that its center lies on the axis of bigger ring at a distance x from the center of bigger ring and its plane is perpendicular to that axis. The mutual inductance of the bigger ring due to the smaller ring is
View Solutiona circular ring carries a chargeQ1 the variation of electric field with distance x measured from centre along Axis for x>>R can be given as (R radius of ring)
View Solution
