During current growth in an L-R circuit the time constant is the time in which the magnitude of current becomes
i0
i0/2
0.63i0
0.37i0
The correct Answer is:C
To solve the question regarding the time constant in an L-R circuit, we will go through the following steps:
Step 1: Understand the L-R Circuit
An L-R circuit consists of an inductor (L) and a resistor (R) connected in series with a battery of electromotive force (E). The inductor stores energy in the magnetic field when current flows through it, while the resistor dissipates energy as heat.
Hint: Remember that the inductor's behavior is characterized by its inductance (L) and the resistor's behavior is characterized by its resistance (R).
Step 2: Define the Current in the Circuit
The current (I) at any time (t) in the L-R circuit can be expressed by the formula:
I(t)=I0(1−e−RtL)
where:
- I0 is the maximum current (steady-state current) given by I0=ER,
- e is the base of the natural logarithm.
Hint: The term e−RtL represents the exponential decay of the current growth in the circuit.
Step 3: Define the Time Constant
The time constant (τL) for an L-R circuit is defined as:
τL=LR
This time constant indicates the time it takes for the current to reach approximately 63.2% of its maximum value (I0).
Hint: The time constant is a crucial parameter that helps in understanding how quickly the circuit responds to changes in voltage.
Step 4: Calculate the Current at One Time Constant
To find the current at one time constant (t=τL):
I(τL)=I0(1−e−1)
Since e−1 is approximately 0.3679, we can calculate:
I(τL)=I0(1−0.3679)
I(τL)≈I0×0.6321
Hint: The value 1−e−1 gives you the fraction of the maximum current reached after one time constant.
Step 5: Conclusion
After one time constant, the magnitude of the current becomes approximately 0.63 times the initial current I0. Thus, the correct answer to the question is:
Current at τL=0.63I0
Final Answer: The time constant is the time in which the magnitude of current becomes 0.63I0.
An L-R circuit consists of an inductor (L) and a resistor (R) connected in series with a battery of electromotive force (E). The inductor stores energy in the magnetic field when current flows through it, while the resistor dissipates energy as heat.
The current (I) at any time (t) in the L-R circuit can be expressed by the formula:
I(t)=I0(1−e−RtL)
where:
- I0 is the maximum current (steady-state current) given by I0=ER,
- e is the base of the natural logarithm.
The time constant (τL) for an L-R circuit is defined as:
τL=LR
This time constant indicates the time it takes for the current to reach approximately 63.2% of its maximum value (I0).
To find the current at one time constant (t=τL):
I(τL)=I0(1−e−1)
Since e−1 is approximately 0.3679, we can calculate:
I(τL)=I0(1−0.3679)
I(τL)≈I0×0.6321
After one time constant, the magnitude of the current becomes approximately 0.63 times the initial current I0. Thus, the correct answer to the question is:
Current at τL=0.63I0
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
For L-R circuit, the time constant is equal to
View SolutionDuring current growth in L-R circuit, match the following table,

View SolutionThe figure shows an L−R circuit the time constant for the circuit is
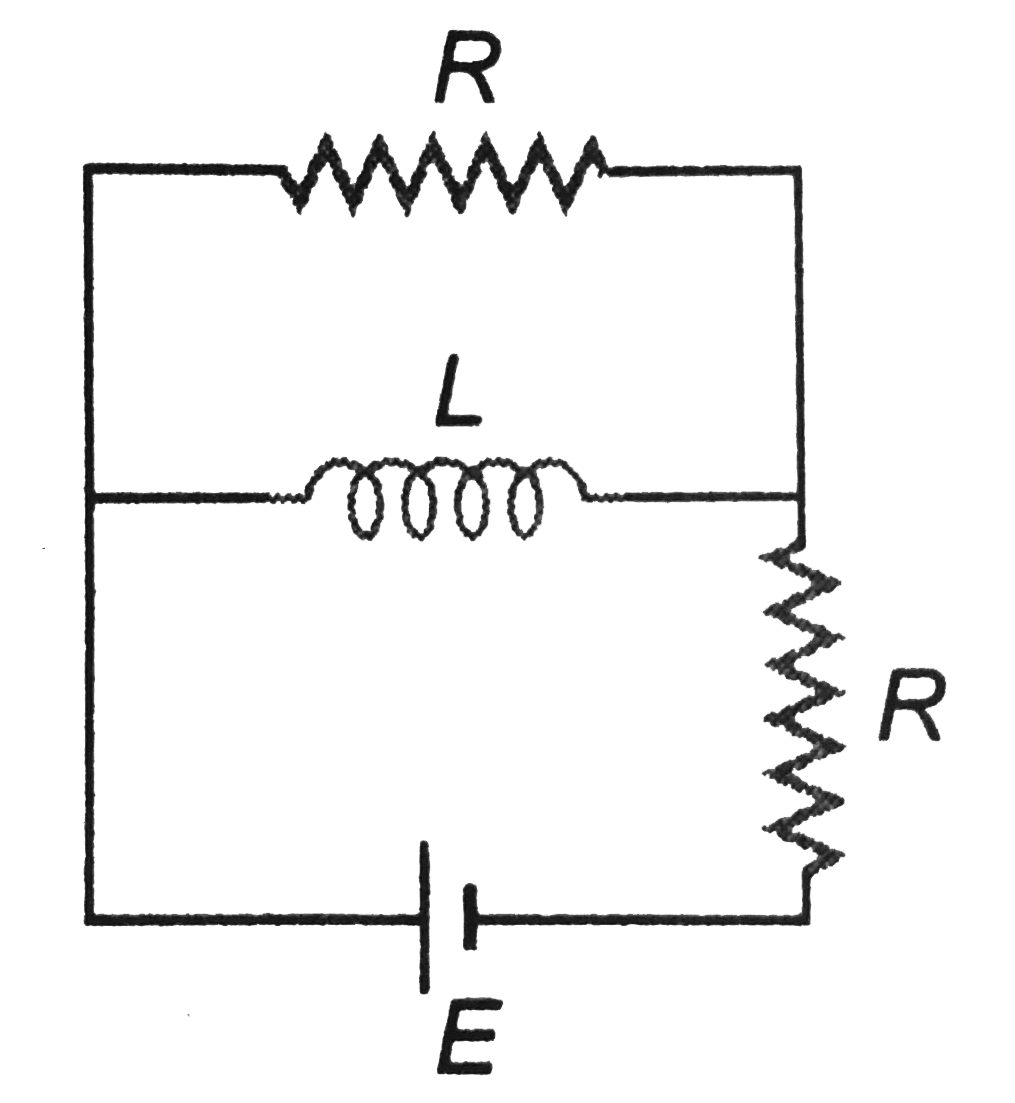
View SolutionThe time constant of C-R circuit is
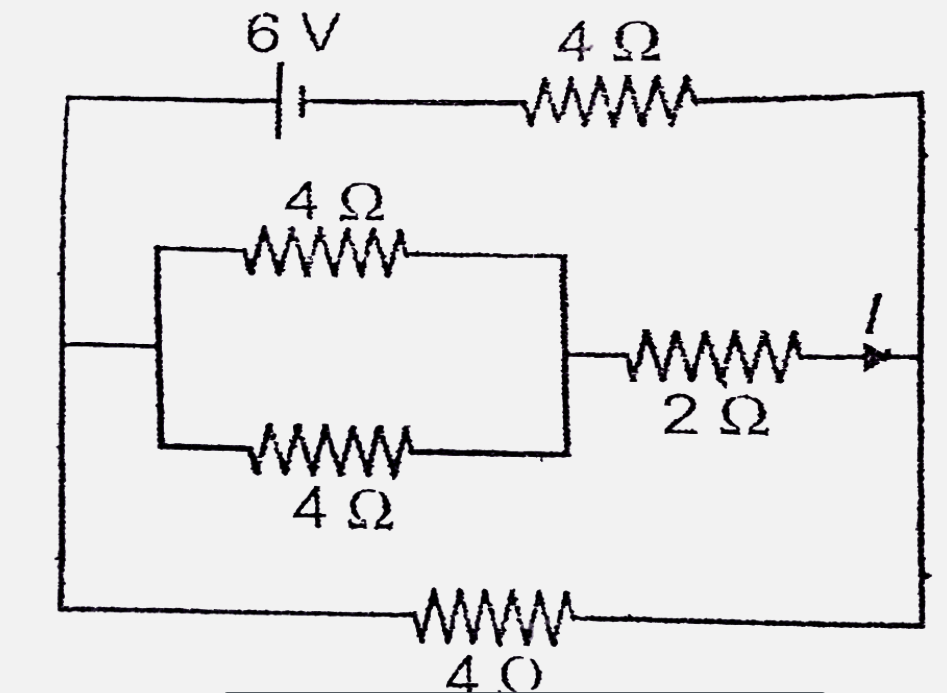
View SolutionThe current l in the circuit shown below is
View SolutionA current i0 is flowing through an L−R circuit of time constant t0. The source of the current is switched off at time t=0. Let r be the value of (−di/dt) at time t=0.Assuming this rate to be constant, the current will reduce to zero in a time interval of
View Solution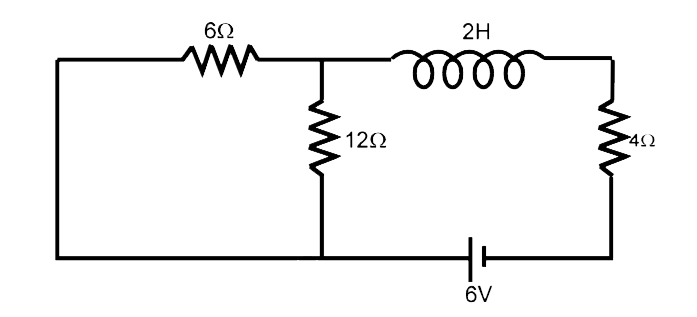
In the circuit shown in figure, time constant and steady state current will be
View SolutionThe time constant of and R- C cirucit during charging is them time in which the charge on the condenser plates, as compared to maximum charge (q0) becomes (q/q0)×100, which is equal to …….. .
View SolutionIn Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is
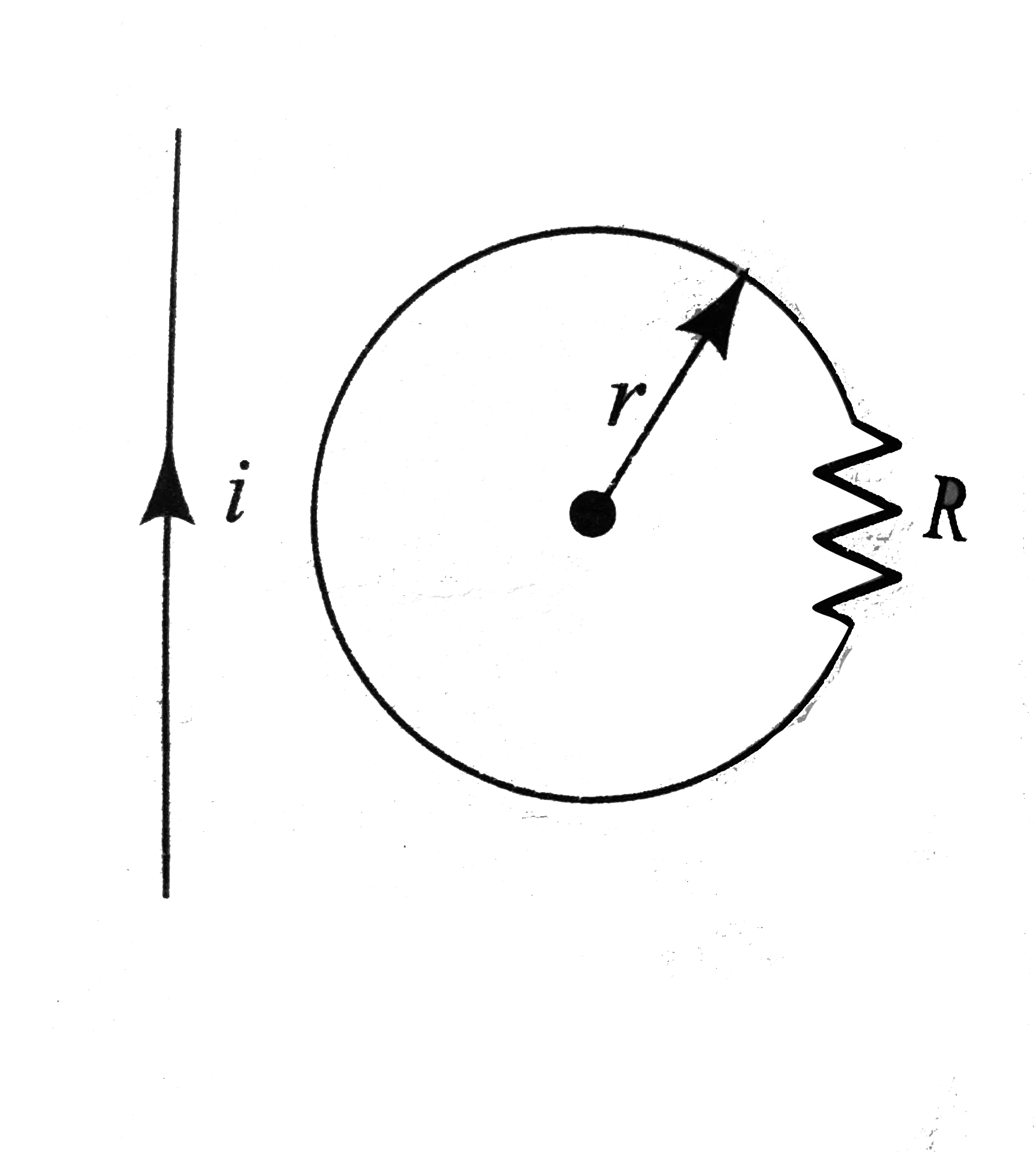
View SolutionThe time constant of L-R circuit is doubled if
View Solution
