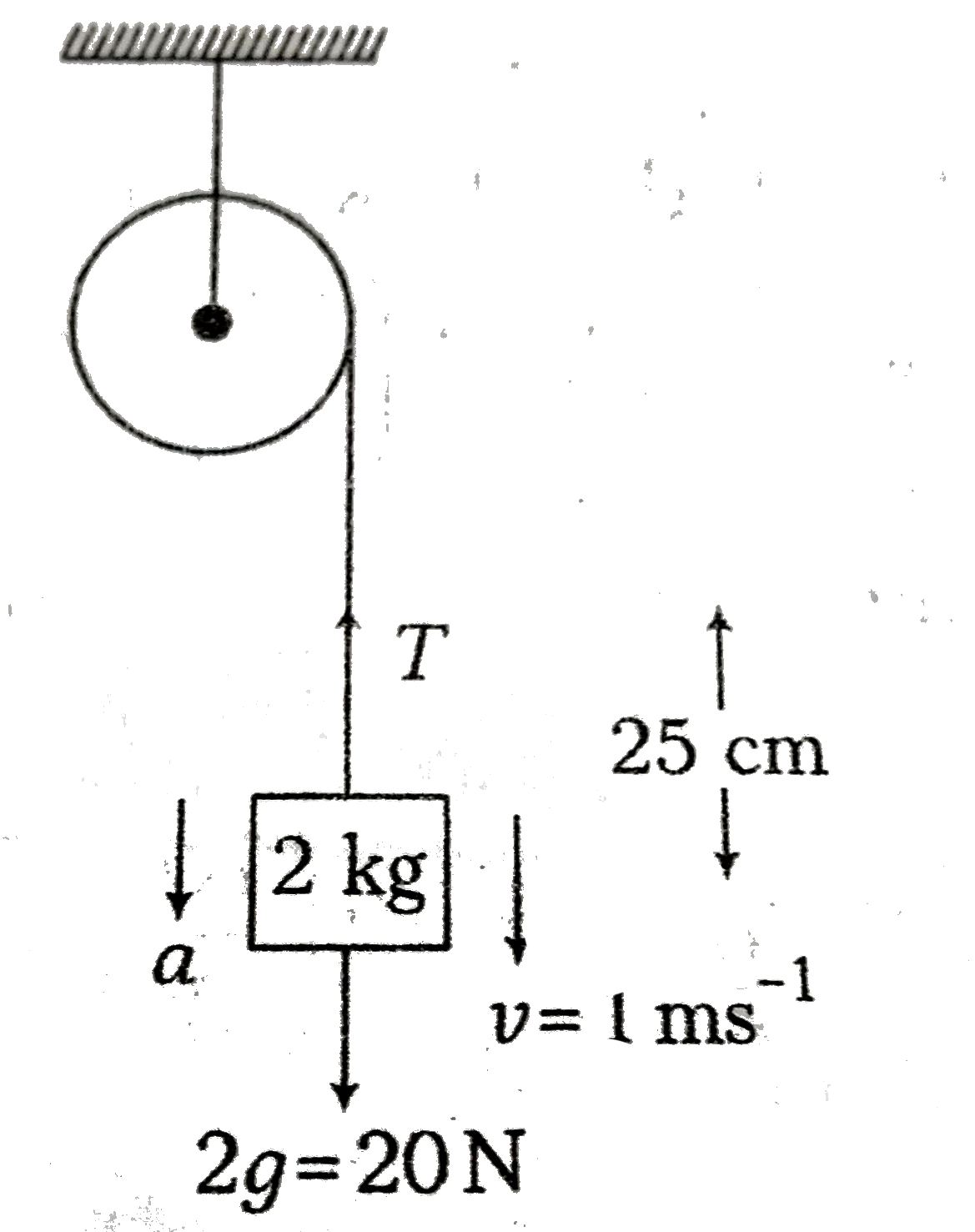
A mass of 3kg descending vertically downwards supports a mass of 2kg by means of a light string passing over a pulley At the end of 5s the string breaks How much high from now the 2kg mass will go (g=9.8m/2).
4.9 m
9.8m
10.6 m
2.45 m
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the two masses connected by a string over a pulley.
Step 1: Understand the system
We have two masses:
- Mass m1=3kg (descending)
- Mass m2=2kg (ascending)
The mass m1 is descending, which means it is accelerating downwards, while m2 is moving upwards with the same acceleration due to the tension in the string.
Step 2: Write the equations of motion
For mass m1 (3 kg):
- The net force acting on it is 3g−T (where T is the tension in the string).
- According to Newton's second law, this net force equals the mass times acceleration:
3g−T=3a(1)
For mass m2 (2 kg):
- The net force acting on it is T−2g.
- Again, applying Newton's second law:
T−2g=2a(2)
Step 3: Solve for acceleration a
We can add equations (1) and (2) to eliminate T:
(3g−T)+(T−2g)=3a+2a
This simplifies to:
3g−2g=5a
Thus:
g=5a⇒a=g5
Step 4: Calculate the upward velocity of m2 after 5 seconds
Now, we need to find the velocity of mass m2 after 5 seconds. Using the formula:
v=u+at
where u=0 (initial velocity), a=g5, and t=5s:
v=0+(g5)⋅5=g
Thus, the velocity of mass m2 after 5 seconds is g.
Step 5: Analyze the motion after the string breaks
When the string breaks, mass m2 will continue to move upwards with the velocity g but will be acted upon only by gravity, which will decelerate it.
Using the equation of motion:
v2=u2+2as
where:
- v=0 (final velocity at the highest point),
- u=g (initial velocity just after the string breaks),
- a=−g (acceleration due to gravity, acting downwards).
Substituting these values:
0=g2+2(−g)s
This simplifies to:
0=g2−2gs⇒2gs=g2⇒s=g2
Step 6: Calculate the height s
Substituting g=9.8m/s2:
s=9.82=4.9m
Final Answer
The height from now that the 2kg mass will go after the string breaks is 4.9 meters.
---
We have two masses:
- Mass m1=3kg (descending)
- Mass m2=2kg (ascending)
For mass m1 (3 kg):
- The net force acting on it is 3g−T (where T is the tension in the string).
- According to Newton's second law, this net force equals the mass times acceleration:
3g−T=3a(1)
- The net force acting on it is T−2g.
- Again, applying Newton's second law:
T−2g=2a(2)
We can add equations (1) and (2) to eliminate T:
(3g−T)+(T−2g)=3a+2a
This simplifies to:
3g−2g=5a
Thus:
g=5a⇒a=g5
Now, we need to find the velocity of mass m2 after 5 seconds. Using the formula:
v=u+at
where u=0 (initial velocity), a=g5, and t=5s:
v=0+(g5)⋅5=g
Thus, the velocity of mass m2 after 5 seconds is g.
When the string breaks, mass m2 will continue to move upwards with the velocity g but will be acted upon only by gravity, which will decelerate it.
v2=u2+2as
where:
- v=0 (final velocity at the highest point),
- u=g (initial velocity just after the string breaks),
- a=−g (acceleration due to gravity, acting downwards).
0=g2+2(−g)s
This simplifies to:
0=g2−2gs⇒2gs=g2⇒s=g2
Substituting g=9.8m/s2:
s=9.82=4.9m
The height from now that the 2kg mass will go after the string breaks is 4.9 meters.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns7videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.420videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
Three equal weights of 3 kg each are hanging on a string passing over a frictionless pulley as shown in figure. The tension in the string between masses II and III will be (Take = 10m/sec2)
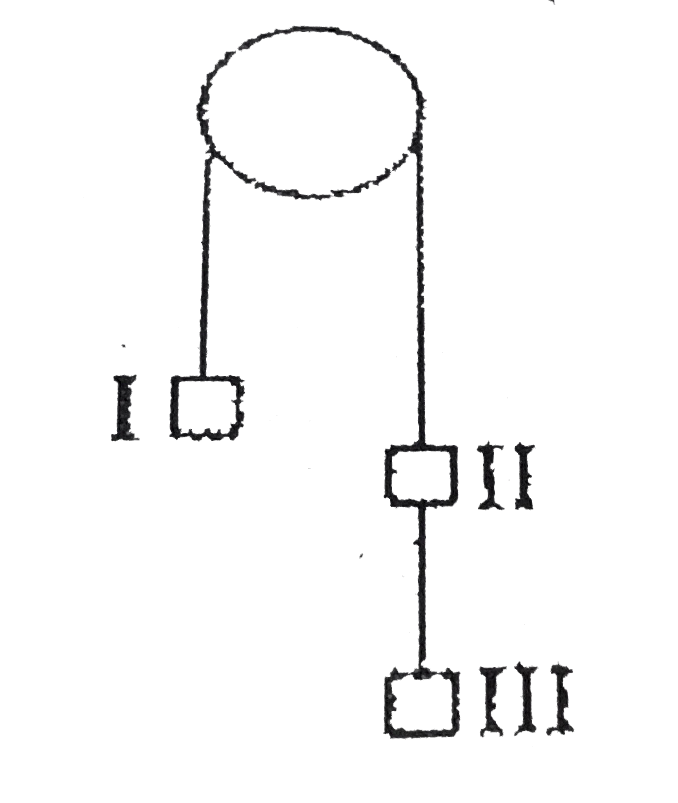 View Solution
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
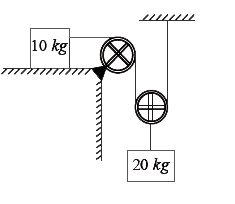 View Solution
View SolutionA mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
View SolutionTwo masses 5 kg and 3 kg are suspended from the ends of an unstretchable light string passing over a frictionless pulley. When the masses are released, the thrust on the pulley is (g = 10ms−2)
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
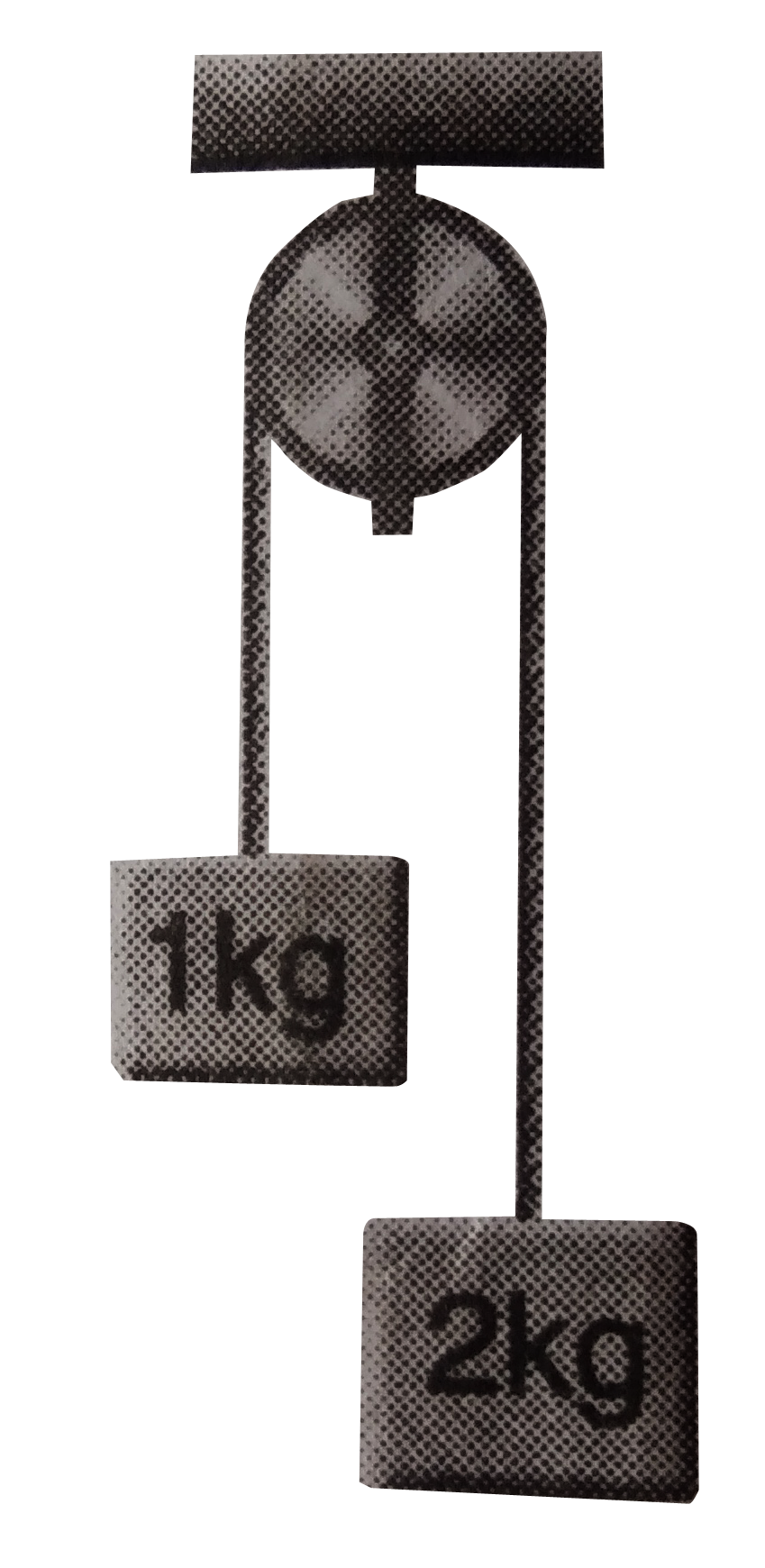 View Solution
View SolutionA block of mass 5kg is hung with the help of light string which is passing over an ideal pulley as shown as in figure.The force is exerted by the clamp on the pulley will be (g= 10 m/s^2)
_PHY_E05_165_Q01.png) View Solution
View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)
 View Solution
View Solution

