Pushing force making an angle θ to the horizontal is applied on a block of weight W placed on a horizontal table . If the angle of friction is ϕ , magnitude of force required to move the body is equal to :
wcosθcos(θ−ϕ)
wsinθcos(θ+ϕ)
wtanϕsin(θ+ϕ)
wsinϕtan(θ+ϕ)
The correct Answer is:B
(b) N=w=Fsinθ
∴ fmax=μN=(tanϕ)(w+Fsinθ)
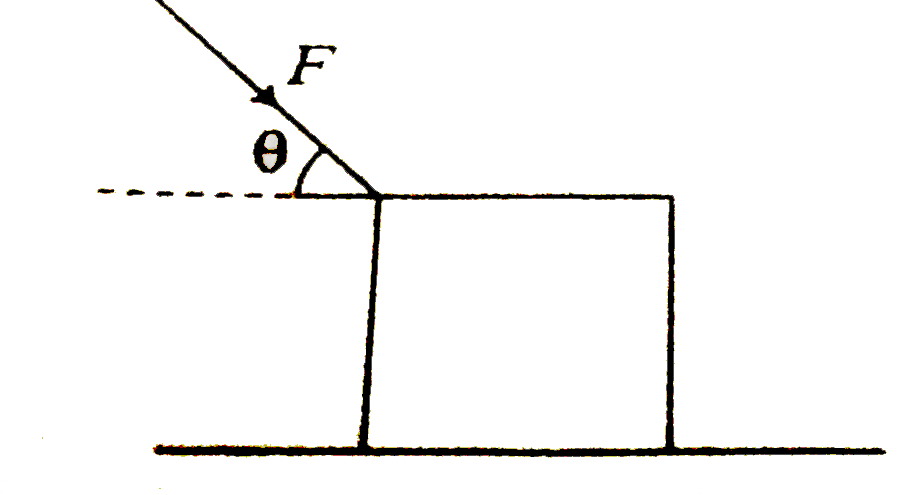
To move the body,
Fcosθ=fmax=(tanϕ)(w+Fsinθ)
Solving this equation we get,
F=wsinθcos(θ+ϕ)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
If a pushing force making an angle α with horizontal is applied on a block of mass m placed on horizontal table and angle of friction is β, then minimum magnitude of force required to move the block is
View SolutionA weight W rests on a rough horizontal plane,If the angle of friction is θ,the least force that can move the body along the plane will be
View SolutionA body of mass 10 kg is placed on rough surface, pulled by force F making an angle of 30∘ above the horizontal. If the angle of friction is also 30∘, then the minimum magnitude of force F required to move the body is equal to ( take, g=10ms−2)
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View SolutionA force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of weight 100N is lying on a rough horizontal surface. If coefficient of friction 1/√3. The least possible force that can move the block is
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View Solution
