Self - inductance 0.8×10−4H of a uniformly wound solenoid, having resistance 3 Ω is broken up into two indentical coils. Those coils are connected in series across a 6 V battery of negligible resistance. Find time constant and steady state current.
To solve the problem, we need to find the time constant and steady-state current for the given solenoid after it has been broken into two identical coils and connected in series across a battery.
1. Identify Given Values:
- Self-inductance of the solenoid, L=0.8×10−4H
- Resistance of the solenoid, R=3Ω
- Voltage of the battery, V=6V
2. Determine New Inductance after Breaking:
- When the solenoid is broken into two identical coils, the inductance of each coil becomes half of the original inductance.
L′=L2=0.8×10−42=0.4×10−4H
3. Determine New Resistance after Breaking:
- The resistance of each coil remains the same because the material and dimensions do not change. Therefore, the total resistance when connected in series is:
R′=R+R=3+3=6Ω
4. Calculate Total Inductance in Series:
- The total inductance when the two coils are connected in series is:
Leq=L′+L′=0.4×10−4+0.4×10−4=0.8×10−4H
5. Calculate Time Constant (τ):
- The time constant for an RL circuit is given by:
τ=LeqR′
Substituting the values:
τ=0.8×10−46=0.86×10−4≈1.33×10−5s
6. Calculate Steady-State Current (I):
- The steady-state current can be calculated using Ohm's law:
I=VR′
Substituting the values:
I=66=1A
Final Results:
- Time constant, τ≈1.33×10−5s
- Steady-state current, I=1A
- Self-inductance of the solenoid, L=0.8×10−4H
- Resistance of the solenoid, R=3Ω
- Voltage of the battery, V=6V
- When the solenoid is broken into two identical coils, the inductance of each coil becomes half of the original inductance.
L′=L2=0.8×10−42=0.4×10−4H
- The resistance of each coil remains the same because the material and dimensions do not change. Therefore, the total resistance when connected in series is:
R′=R+R=3+3=6Ω
- The total inductance when the two coils are connected in series is:
Leq=L′+L′=0.4×10−4+0.4×10−4=0.8×10−4H
- The time constant for an RL circuit is given by:
τ=LeqR′
Substituting the values:
τ=0.8×10−46=0.86×10−4≈1.33×10−5s
- The steady-state current can be calculated using Ohm's law:
I=VR′
Substituting the values:
I=66=1A
- Time constant, τ≈1.33×10−5s
- Steady-state current, I=1A
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together119videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective20videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A uniformly wound solenoid coil of self inductance 1.8×10−4H and resistance 6Ω is broken up into two identical coils. These identical coils are then connected in parallel across a 12V battery of negligible resistance. The time constant and steady state current will be
View SolutionA uniform wound solenoidal coil of self inductance 1.8×10−4 henry and resistance 6 ohm is broken up into two identical coils. These identical coils are then connected in parallel across a 15-volt battery of negligible resistance. The time constant for the current in the circuit is.......seconds and the steady state current through the battery is ..............amperes.
View SolutionA uniformly wound solenoid coil of slf inductnace 4 mH and resistance 12Ω is broken int two parts. These two coil are connected in parallel across is 12V battery. The steady current through battery is
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate :the current through the battery
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate :the current through each resistor
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate : (a) the total resistance of the circuit,
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power supplied by the battery,View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power dissipated in each resistor.View SolutionThe figure shows two capacitors connected in parallel with two resistance and a battery of emf 10V , internal resistance 5Ω. At steady state.
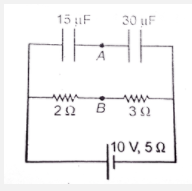 View Solution
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The time constant of the circuitView Solution

