Space is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
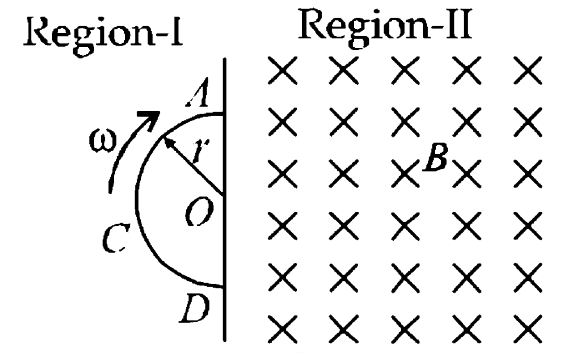
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
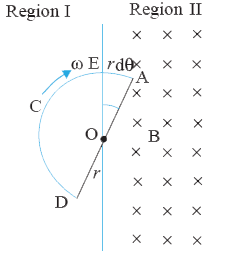
When the loop is in region I, the magnetic field linked with the loop is zero. When the loop enters in magnetic field in region II. the magnetic flux linked with it, is given by<br>ϕ=BA
therefore e.m.f inducedε=-(dphi)/(dt)=-(d(BA))/(dt)<br≥-B(dA)/(dt)=B(dA)/(dt)Letdthe≠bethe∠rotatedbythel∞p∈timedt,thendA=Areaofthe△OEA=(12)r.r.dthη∴epsilonB.(1)/(2).(r.rd theta)/(dt)=(1)/(2)Br^(2)((d theta)/(dt)=(1)Br^(2)omega<br>Inducedcurrent=(e.m.r)/(R)=(1)/(2)(Br^(2)0mega)/(R)dAcanalsobecalca––ted∈thefollow∈gway:Theareacorrespond∈g2pi (angle)isispi r^(2)<br>∴areacorrespond∈g→unit∠<br>areacorrespond∈g→∠dtheta=(pir^(2))/(2r)xxdthetatherefore dA=(pi^(2))/(2r)xxdtheta=(1)/((2)r^(2)dtheta
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - SOLVED EXAMPLES
24 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 1
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
A uniform but time-varying magnetic field B(t) exists in a cylindrical region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
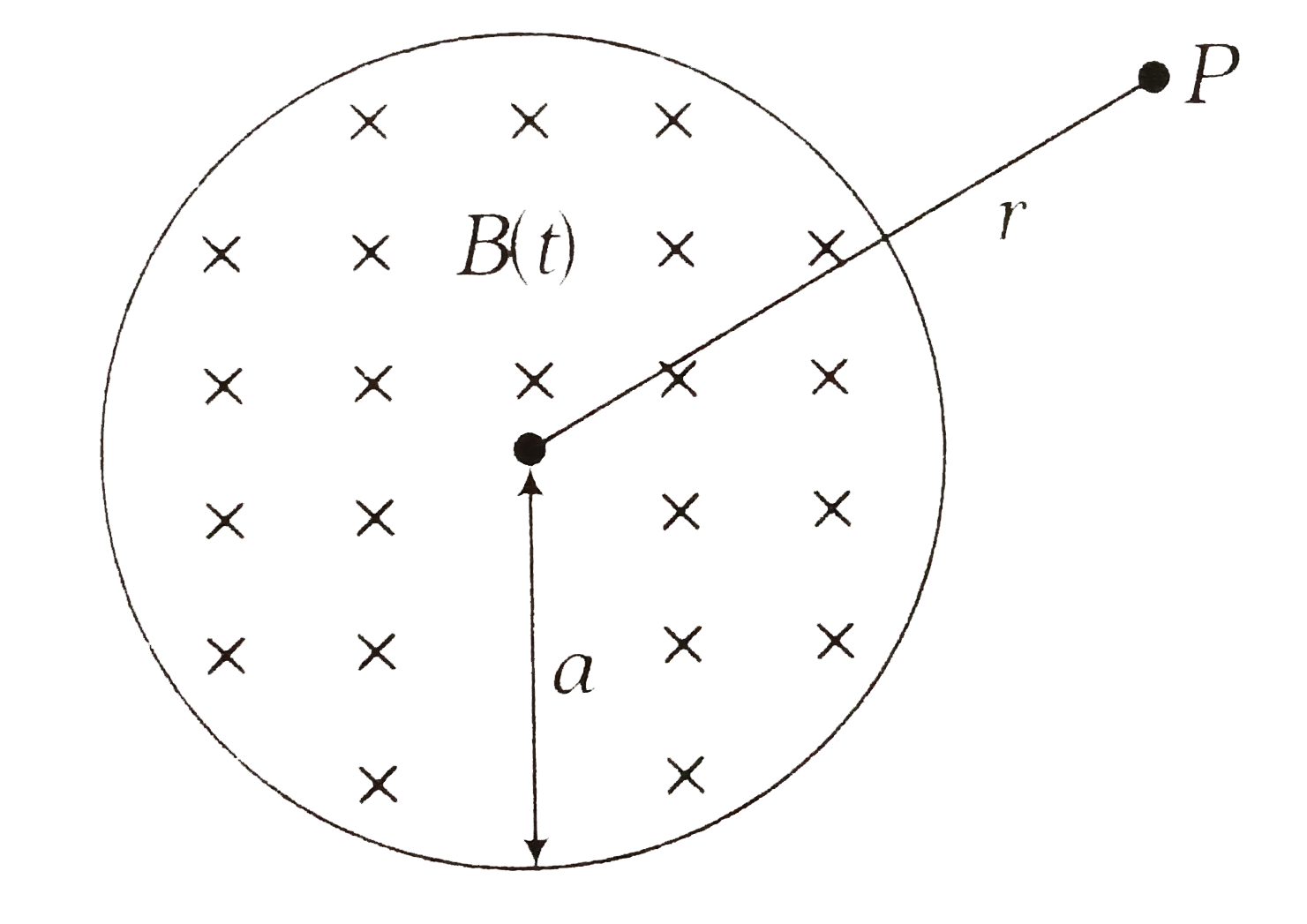
View SolutionWhen ever the flux linked with a coil changes, then
View SolutionIf a ship of mass 4×107 kg initially at rest is pulled by a force of 5×104 N through a distance of 4 m, then the speed of the ship will be (resistance due to water is negligible )
View SolutionThe turn ratio of a transformers is given as 2:3. If the current through the primary coil is 3A, thus calculate the current through load resistance
View SolutionA wire loop confined in a plane is rotated in its oen plane with some angular velocity. A uniform magnetic field exists in the region. Fid the emf induced in the loop.
View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity omega about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R. (i) obtain an expression for hte magnitude of the induced cureent in the loop. (ii) Show the direction of the current when the loop is entering into the Rigion II. Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionA square loop of wire carrying current I is lying in the plane of paper as shown in Fig. 1.141. The magnetic field is present in the region as shown. The loop will tend to rotate
View SolutionThere is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R. Obtain an expression for the magnitude of the induced current in the loop.
View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R. Show the direction of the current when the loop is entering into the region II.
View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R. Plot a graph between the induced emf and the time of rotation for two periods of rotation.
View SolutionThere is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
View SolutionThe magnetic field B shown in is directed into the plane of the paper. ACDA is a semicircular conducting loop of radius r with the centre at O. The loop is now made ot rotate clockwise with a constant angular velocity ω about on axis passing through O and perpendicular to the plane of the paper. The resistance of the loop is R. Obtain an expression for the magnitude of the induced current in the loop. Plot a graph between the induced current i and ωt, for two periods of rotation.

View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
View SolutionThere is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
View Solution
