A coil of 40Ω resistance has 100 turns and radius 6mm us connected to ammeter of resistance of 160ohms. Coil is placed perpendicular to the magnetic field. When coil is taken out of the field, 32μC charge flows through it. The intensity of magnetic field will be
6.55 T
5.66 T
2.55 T
0.566 T
The correct Answer is:D
To find the intensity of the magnetic field when a coil is taken out of the field, we can use the relationship between induced EMF, resistance, charge, and the area of the coil. Here’s a step-by-step solution:
Step 1: Calculate the Total Resistance
The total resistance Rtotal in the circuit is the sum of the coil's resistance and the ammeter's resistance.
Rtotal=Rcoil+Rammeter=40Ω+160Ω=200Ω
Hint: Remember to add the resistances in series.
Step 2: Use Faraday's Law of Electromagnetic Induction
According to Faraday's law, the induced EMF (E) in the coil is given by:
E=−dΦdt⋅N
Where:
- Φ is the magnetic flux,
- N is the number of turns in the coil.
Since the coil is taken out of the magnetic field, the initial magnetic flux is 0 and the final flux is determined by the magnetic field B and the area A of the coil.
Step 3: Calculate the Area of the Coil
The area A of the coil can be calculated using the formula for the area of a circle:
A=πr2
Given the radius r=6mm=6×10−3m:
A=π(6×10−3)2=π(36×10−6)=36π×10−6m2
Hint: Convert all measurements to SI units before performing calculations.
Step 4: Relate Induced EMF to Charge and Resistance
The induced EMF can also be expressed in terms of the charge Q that flows through the circuit and the total resistance:
E=I⋅Rtotal=QΔt⋅Rtotal
Where Q=32μC=32×10−6C.
Step 5: Calculate the Current
Since we are not given the time Δt, we can rearrange the equation to find the induced EMF:
E=QΔt⋅Rtotal
Step 6: Substitute into Faraday's Law
From Faraday's law, we have:
E=N⋅ΔΦΔt
Where ΔΦ=B⋅A. Therefore, we can equate:
QΔt⋅Rtotal=N⋅B⋅A
Step 7: Solve for the Magnetic Field B
Rearranging gives:
B=Q⋅RtotalN⋅A
Substituting the values:
- Q=32×10−6C
- Rtotal=200Ω
- N=100
- A=36π×10−6m2
B=32×10−6⋅200100⋅36π×10−6
Step 8: Simplify the Expression
B=6400×10−63600π×10−6=64003600π=89πT
Final Answer
Thus, the intensity of the magnetic field B is:
B≈89πT
Hint: Ensure to simplify fractions carefully and check units for consistency.
The total resistance Rtotal in the circuit is the sum of the coil's resistance and the ammeter's resistance.
According to Faraday's law, the induced EMF (E) in the coil is given by:
- Φ is the magnetic flux,
- N is the number of turns in the coil.
The area A of the coil can be calculated using the formula for the area of a circle:
The induced EMF can also be expressed in terms of the charge Q that flows through the circuit and the total resistance:
Since we are not given the time Δt, we can rearrange the equation to find the induced EMF:
From Faraday's law, we have:
Rearranging gives:
- Rtotal=200Ω
- N=100
- A=36π×10−6m2
B=6400×10−63600π×10−6=64003600π=89πT
Thus, the intensity of the magnetic field B is:
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A closed coil consists of 500 turns has area 4cm2 and a resistance of 50Ω. The coil is kept with its plane perpendicular to a uniform magnetic field of 0.2Wbm2. Calculate the amount charge flowing through the coil if it is rotated through 180∘
View SolutionA rectangular coil of area 50cm2 and 100 turns is placed perpendicular to a magnetic field of 10−2Wb/m2. If the coil is withdrawn from the field in 40 ms, calculate the emf induced.
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular coil of 20 turns and area of cross-section 25cm2 has a resistance of 100ohm. If a magnetic field which is perpendicular to the plane of the coil changes at the rate of 1000 telsa per second, the current in the coil is
A1AB50 AC0.5AD5A
Initially plane of coil is parallel to the uniform magnetic field B. In time Δt it makes to perpendicular to the magnetic field, then charge flows in Δt depends on this time as -
View SolutionA coil of inductance 1.0 H and resistance 100 Omega is connected to a battery of emf 12 V. Find the energy stored in the magnetic field associated with the coil at an instant 10 ms after the circuit is switched on.
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
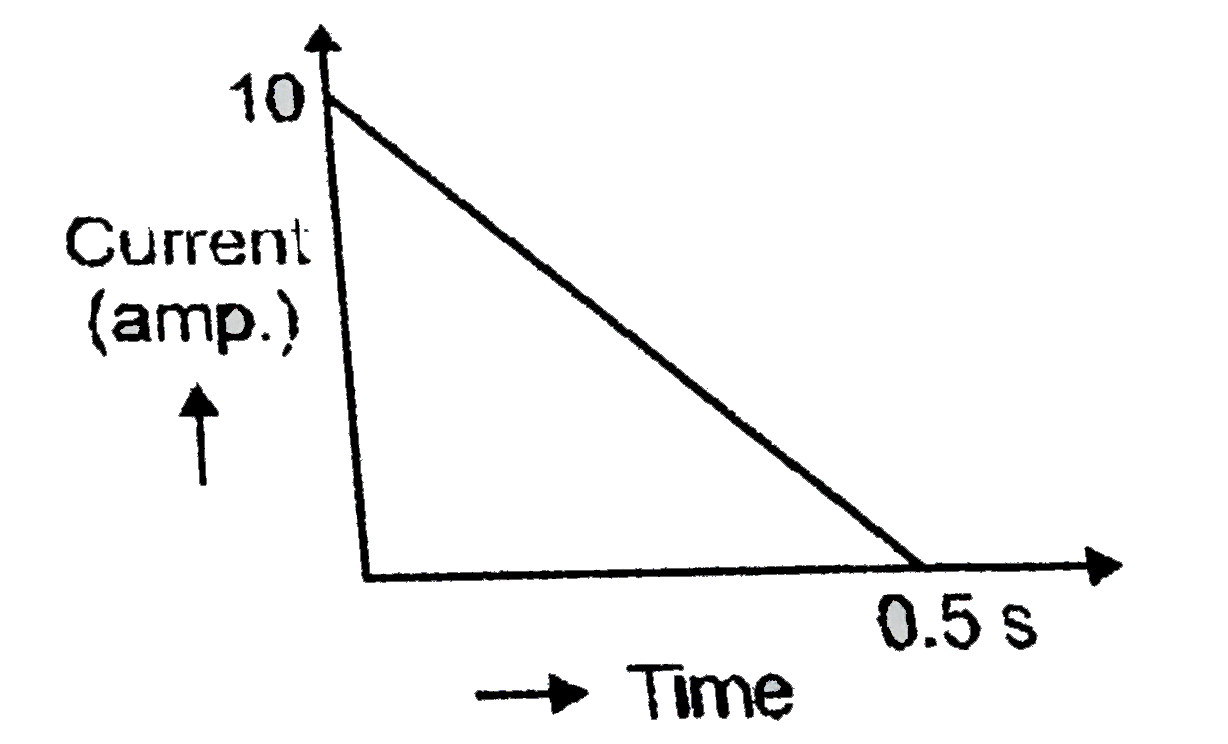 View Solution
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
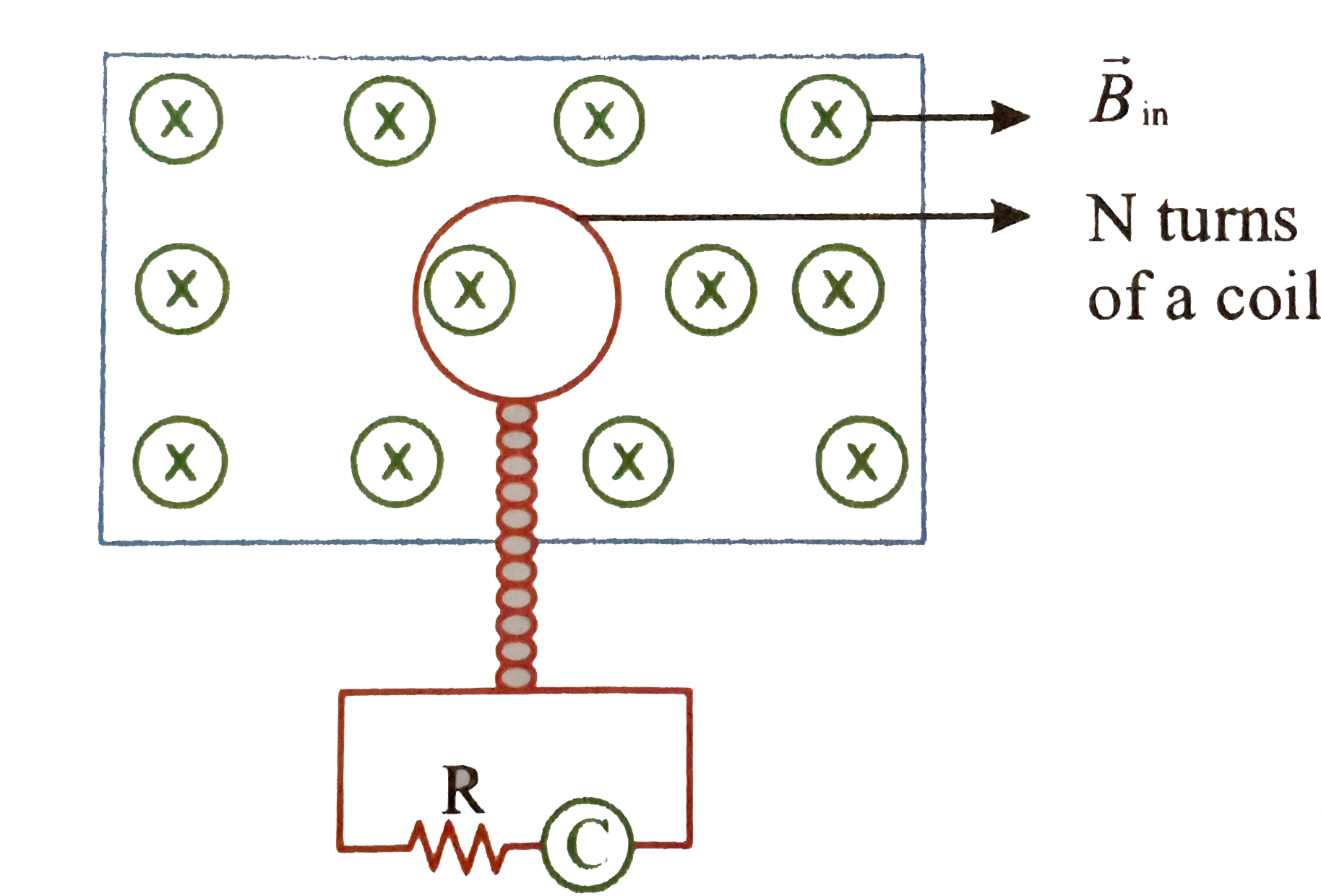 View Solution
View SolutionA flat coil, C, of n turns, area A and resistance R, is placed in a uniform magnetic field of magnitude B. The plane of the coil is initially perpendicular to B. The coil,is rotated by an angle θ about a diameter and charge of amount Q flows through it. Choose the correct alternatives.
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the
 View Solution
View SolutionA coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
View Solution

