shows a conducting loop being pulled out of a magnetic field with a speed v. Which of lthe four plots shown in may represent the power delivered by the pulling agent as a function of the speed v ?
a
b
c
d
a
b
c
d
The correct Answer is:B
To solve the problem of determining which plot represents the power delivered by the pulling agent as a function of speed v for a conducting loop being pulled out of a magnetic field, we can follow these steps:
1. Understand the Induced EMF:
The induced electromotive force (EMF) in the loop can be expressed using Faraday's law of electromagnetic induction. For a loop being pulled out of a magnetic field with a velocity v, the induced EMF (E) is given by:
E=B⋅L⋅v
where B is the magnetic field strength, L is the length of the loop, and v is the velocity.
Hint: Remember that the induced EMF is directly proportional to the velocity of the loop.
2. Calculate the Power:
The power (P) delivered by the pulling agent can be calculated using the formula:
P=E2R
where R is the resistance of the loop. Substituting the expression for EMF, we get:
P=(B⋅L⋅v)2R
3. Simplify the Power Expression:
Simplifying the expression for power, we have:
P=B2⋅L2⋅v2R
This shows that power P is proportional to the square of the velocity:
P∝v2
Hint: Identify the relationship between power and velocity; it is quadratic.
4. Determine the Graph Shape:
Since P is proportional to v2, the graph of power versus velocity will be a parabola opening upwards. This means as the velocity increases, the power increases with the square of the velocity.
5. Select the Correct Plot:
Among the given options (a, b, c, d), we need to identify which one represents a parabolic relationship. The correct plot will show a curve that starts at the origin and rises steeply as v increases.
Hint: Look for a graph that resembles a quadratic function, typically shaped like a "U".
Conclusion:
Based on the analysis, the correct option that represents the power delivered by the pulling agent as a function of speed v is option B, which shows a parabolic relationship.
The induced electromotive force (EMF) in the loop can be expressed using Faraday's law of electromagnetic induction. For a loop being pulled out of a magnetic field with a velocity v, the induced EMF (E) is given by:
E=B⋅L⋅v
where B is the magnetic field strength, L is the length of the loop, and v is the velocity.
The power (P) delivered by the pulling agent can be calculated using the formula:
P=E2R
where R is the resistance of the loop. Substituting the expression for EMF, we get:
P=(B⋅L⋅v)2R
Simplifying the expression for power, we have:
P=B2⋅L2⋅v2R
This shows that power P is proportional to the square of the velocity:
P∝v2
Since P is proportional to v2, the graph of power versus velocity will be a parabola opening upwards. This means as the velocity increases, the power increases with the square of the velocity.
Among the given options (a, b, c, d), we need to identify which one represents a parabolic relationship. The correct plot will show a curve that starts at the origin and rises steeply as v increases.
Based on the analysis, the correct option that represents the power delivered by the pulling agent as a function of speed v is option B, which shows a parabolic relationship.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Fig. Show a rectangular loop MNOP being pulled out of a magnetic field with a uniform velocity v by applying an external force F. The length MN is equal to l and the total resistance of the loop is R. Find(a) the current in the loop,(b) the magnetic force on the loop, (c) the external force F needed to maintain the velocity, (d) the power delivered by the external force and (e) the thermal power developed in the loop.
 View Solution
View SolutionA triangular loop as shown in the figure is started to being pulled out at t=0 form a uniform magnetic field with a constant velocity v. Total resistancee of the loop is constant and equal to R. Then the variation of power produced in the loop with time will be :
 View Solution
View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
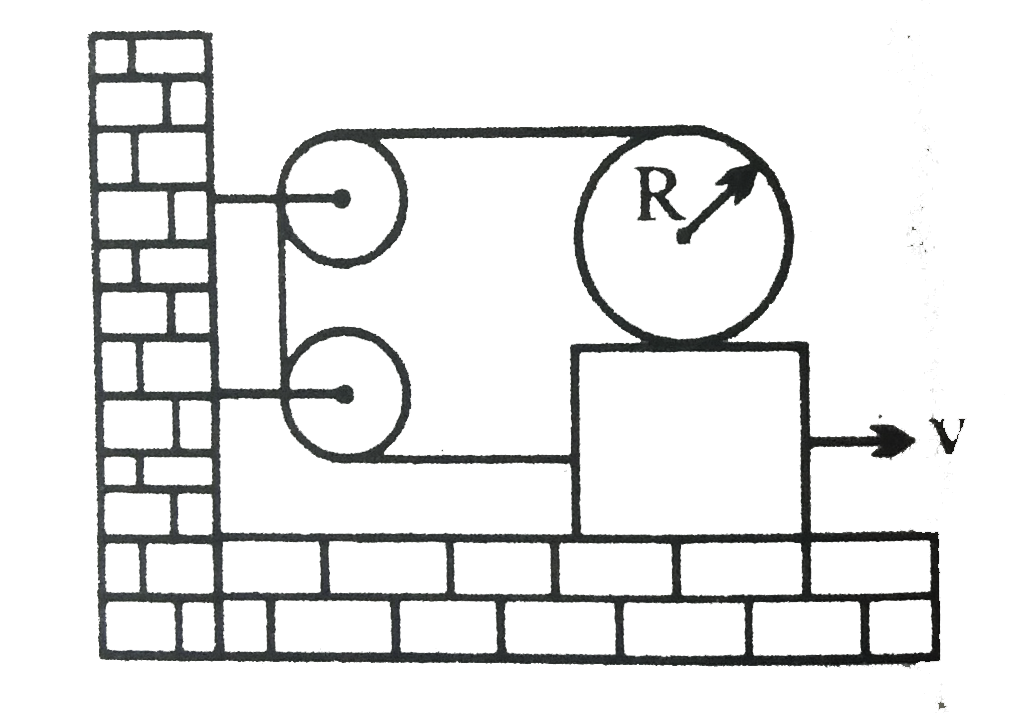 .View Solution
.View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
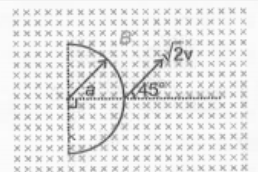 View Solution
View SolutionA conducting loop is pulled with a constant velocity towards a region of unifrom maganetic field of induction B as shown in the figure. Then the current involved in the loop is (d>r)
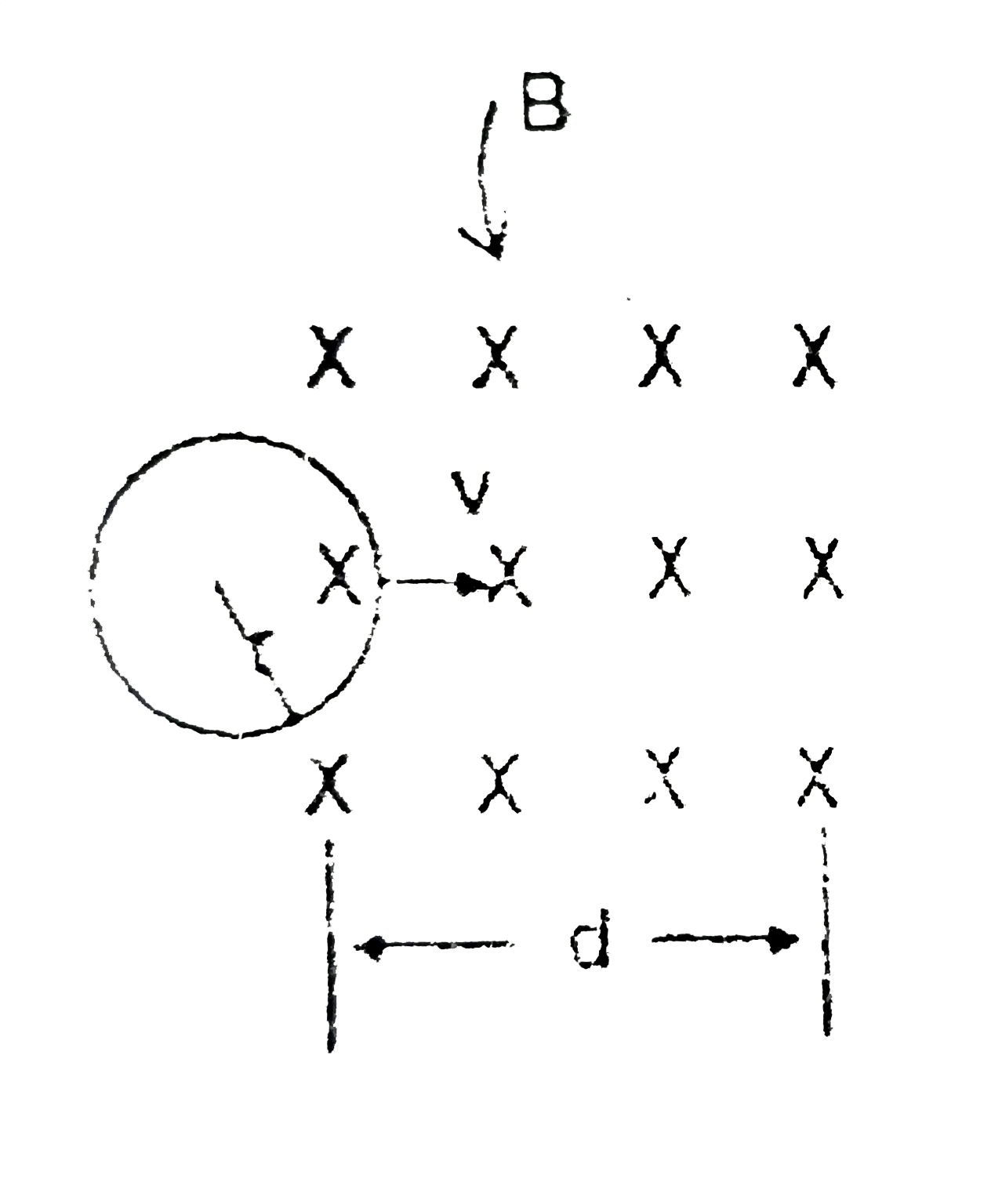 View Solution
View SolutionA conducting rod of length l slides at constant velocity v on two parallel conducting rails, placed in a uniform and constant magnetic field B perpendicular to the plane of the rails as shown in Fig.3.49. A resistance R is connected between the two ends of the rails.

(a) Idenify the cause which produces change in magnetic flux.
(b) Identify the direction of current in the loop.
( c) Determine the emf induced in the loop.
(d) Compute the electric power dissipated in the resistor.
(e) Calcualte the mechenical power required to pull the rod at a cinstant velovity.View SolutionFigure shows a conical conducting wire connected to a source of emf. Let E, vd, I represent the electric field, drift velocity and current at a cross-section of the wire. As one moves from end A to B of the wire
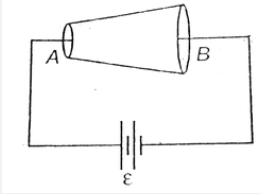 View Solution
View SolutionA wire loop is placed in a region of time varying magnetic field which is oriented orthogonally to the plane of the loop as shown in Fig. The graph shows the magnetic field variation as the function of time. Assume the positive emf is the one which drives a current in the clockwise direction and seen by the observer in the direction of B. Which of the following graphs best represents the induced emf as a function of time?
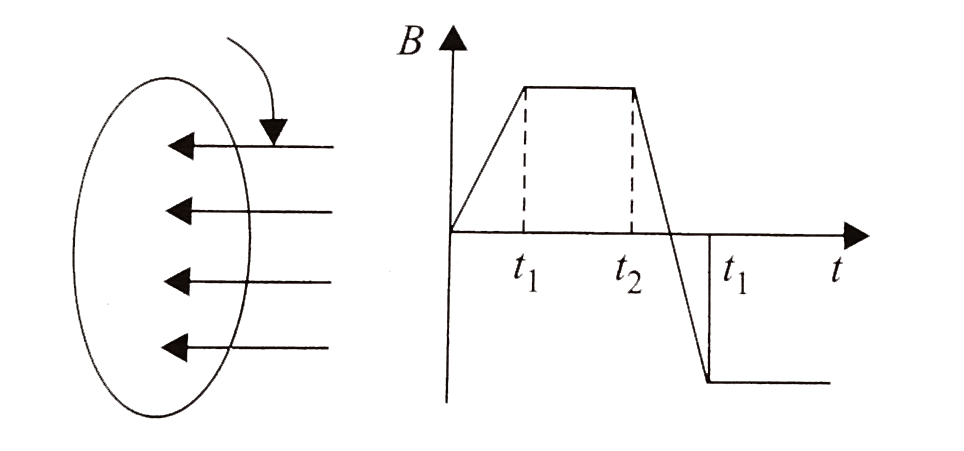 View Solution
View SolutionA rectangular loop and a circular loop are moving out of a uniform magnetic field to a field-free region with a constant velocity 'v' as shown in the figure . Explain the which loop do you expect the induced emf to the constant during the passage out of the field region . The magnetic field is normal to the loops .
View SolutionA conducting loop is moving from left to right through a region of uniform magnetic (B) field. Its four positiors are shown belwo. Show the direction of induced current in all four positions.
 View Solution
View Solution

