In a triangle ABC,∠A=70∘,∠B=80∘ and D is the incentre of ΔABC,∠ACB=2x∘ and ∠BDC=y∘. The values of x and y respectively will be
15∘,130∘
15∘,125∘
35∘,40∘
30∘,150∘
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Find Angle C
In triangle ABC, the sum of the angles is 180 degrees. We know:
- Angle A = 70 degrees
- Angle B = 80 degrees
- Angle C = 2x degrees
Using the angle sum property:
Angle A+Angle B+Angle C=180∘
Substituting the known values:
70∘+80∘+2x=180∘
This simplifies to:
150∘+2x=180∘
Step 2: Solve for x
Now, we can isolate 2x:
2x=180∘−150∘
2x=30∘
Now, divide by 2 to find x:
x=30∘2=15∘
Step 3: Find Angle BDC
Since D is the incenter of triangle ABC, we can use the property of the incenter to find angle BDC (y):
Angle BDC=90∘+Angle A2
Substituting the value of Angle A:
y=90∘+70∘2
Calculating 70∘2:
y=90∘+35∘
y=125∘
Final Answer
Thus, the values of x and y are:
x=15∘andy=125∘
In triangle ABC, the sum of the angles is 180 degrees. We know:
- Angle A = 70 degrees
- Angle B = 80 degrees
- Angle C = 2x degrees
Angle A+Angle B+Angle C=180∘
Substituting the known values:
70∘+80∘+2x=180∘
This simplifies to:
150∘+2x=180∘
Now, we can isolate 2x:
2x=180∘−150∘
2x=30∘
Now, divide by 2 to find x:
x=30∘2=15∘
Since D is the incenter of triangle ABC, we can use the property of the incenter to find angle BDC (y):
Angle BDC=90∘+Angle A2
Substituting the value of Angle A:
y=90∘+70∘2
Calculating 70∘2:
y=90∘+35∘
y=125∘
Thus, the values of x and y are:
x=15∘andy=125∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle ABC,∠A=70∘,∠B=80∘ and D is the incentre of ΔABC.∠ACB=2× and ∠BDC=y∘. The values of x and y, respectively are.
A15, 130B15, 125C35, 40D30, 150 - Question 2 - Select One
I is the incentre of the triangle ABC. If ∠ABC=60∘ and ∠ACB=50∘ then ∠BIC is
A55∘B125∘C70∘D65∘ - Question 3 - Select One
Find the value of x and y respectively, if ΔABC≅ΔQRP.
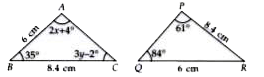 A15∘,30∘B21∘,40∘C30∘,15∘D40∘,21∘
A15∘,30∘B21∘,40∘C30∘,15∘D40∘,21∘
In a triangle ABC, if ∠A=70∘andAB=AC, then find the measures of ∠Band∠C.
View SolutionIn ΔABC if AB=ACand∠B=70∘, then ∠C=2a∘. Find the value of a
View SolutionIn a ΔABC,∠A=2∠B=3∠C, find each of the triangle.
View SolutionIn ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View SolutionIn ΔABC,if BC=AB and ∠B=80∘,then ∠A is equal to
View Solution

