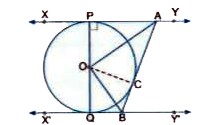
PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
60∘
120∘
90∘
180∘
The correct Answer is:C
To solve the problem, we need to find the angle AOB formed by the tangents AB at points A and B, where PQ and RS are parallel tangents to a circle with center O.
1. Draw the Diagram:
- Start by drawing a circle with center O.
- Draw two parallel tangents PQ and RS to the circle.
- Mark the points where the tangents touch the circle as C (the point of contact for tangent AB).
- Extend the tangent AB such that it intersects PQ at point A and RS at point B.
2. Identify Angles:
- Since PQ and RS are tangents to the circle, the radius OC (from the center O to the point of contact C) is perpendicular to the tangent AB at point C. Therefore, angle OCA = 90° and angle OCB = 90°.
3. Use Properties of Tangents:
- The angles formed by the tangents at points A and B with the line segments OA and OB (i.e., angle OAC and angle OBC) are equal because they are angles made by the same external point A and B with the tangents. Let's denote angle OAC as angle 1 and angle OBC as angle 2.
- Thus, angle 1 = angle 2.
4. Consider the Quadrilateral:
- The angles in quadrilateral formed by points A, B, C, and the center O can be expressed as:
- Angle AOB + angle OAC + angle OBC + angle AOB = 360°.
- Since angle OAC and angle OBC are equal, we can denote them both as angle 1.
- Therefore, the equation simplifies to:
- Angle AOB + 90° + angle 1 + 90° = 360°.
- This means:
- Angle AOB + 180° + 2(angle 1) = 360°.
- Rearranging gives:
- Angle AOB + 2(angle 1) = 180°.
5. Finding Angle AOB:
- Since angle 1 = angle 2, we can substitute angle 2 for angle 1 in the equation:
- Angle AOB + 2(angle 1) = 180°.
- This implies:
- Angle AOB = 180° - 2(angle 1).
- Since angle 1 + angle 2 = 90° (from the properties of angles in a right triangle), we can conclude:
- Angle AOB = 90°.
Conclusion:
Thus, the angle AOB is 90°.
- Start by drawing a circle with center O.
- Draw two parallel tangents PQ and RS to the circle.
- Mark the points where the tangents touch the circle as C (the point of contact for tangent AB).
- Extend the tangent AB such that it intersects PQ at point A and RS at point B.
- Since PQ and RS are tangents to the circle, the radius OC (from the center O to the point of contact C) is perpendicular to the tangent AB at point C. Therefore, angle OCA = 90° and angle OCB = 90°.
- The angles formed by the tangents at points A and B with the line segments OA and OB (i.e., angle OAC and angle OBC) are equal because they are angles made by the same external point A and B with the tangents. Let's denote angle OAC as angle 1 and angle OBC as angle 2.
- Thus, angle 1 = angle 2.
- The angles in quadrilateral formed by points A, B, C, and the center O can be expressed as:
- Angle AOB + angle OAC + angle OBC + angle AOB = 360°.
- Since angle OAC and angle OBC are equal, we can denote them both as angle 1.
- Therefore, the equation simplifies to:
- Angle AOB + 90° + angle 1 + 90° = 360°.
- This means:
- Angle AOB + 180° + 2(angle 1) = 360°.
- Rearranging gives:
- Angle AOB + 2(angle 1) = 180°.
- Since angle 1 = angle 2, we can substitute angle 2 for angle 1 in the equation:
- Angle AOB + 2(angle 1) = 180°.
- This implies:
- Angle AOB = 180° - 2(angle 1).
- Since angle 1 + angle 2 = 90° (from the properties of angles in a right triangle), we can conclude:
- Angle AOB = 90°.
Thus, the angle AOB is 90°.
Topper's Solved these Questions
Similar Questions
In Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
View SolutionXYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View Solution
Knowledge Check
If PQ and PR are two tangents to ta circle with centre O. if ∠QPR=46∘, then ∠QOR is equal to
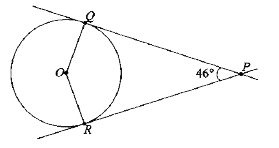 A67∘B46∘C44∘D134∘
A67∘B46∘C44∘D134∘If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
A90∘B45∘C30∘D60∘If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
A90∘B45∘C30∘D60∘
landm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
View SolutionIf Fig , AOB is diameter of a circle with centre O and AC is a tangent to the circle at A . If ∠BOC=130∘ , then find ∠ACO .

View SolutionA is a point at a distance 10 cm from the centre O of a circle of radius 6cm . AP and AQ are the tangents to the circle at P and Q .If a tangent BC is drawn at a point R lying on the mirror are PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC .
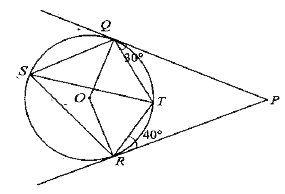
View SolutionIn the figures, PQ and PR are tangents to the circle with centre O. Find RSQ , RTQ , and RˆPQ
View SolutionIn the figure , PQ and PR are tangents drawn from and external point P to the circle with centre O. Q and R are the points of contact. If PQ = 5 cm then what is the length of segment PR ? Why ?

View Solution
