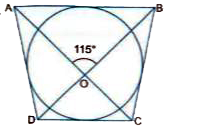
A circle of centre O inscribed in a quadrilateral ABCD which touches all the sides of a quadrilateral. If ∠AOB=115∘. Find ∠COD.
The correct Answer is:65∘
To solve the problem, we need to find the angle ∠COD given that ∠AOB=115∘ in a quadrilateral ABCD with an inscribed circle.
1. Understanding the Geometry:
- We have a quadrilateral ABCD with an inscribed circle centered at point O.
- The circle touches all four sides of the quadrilateral.
2. Identifying Angles:
- We are given that ∠AOB=115∘.
- By the properties of a cyclic quadrilateral (or a quadrilateral with an inscribed circle), the angles at the center formed by the diagonals are related to the angles at the vertices.
3. Using the Property of Opposite Angles:
- The angles at the center O corresponding to opposite sides of the quadrilateral are supplementary. This means:
∠AOB+∠COD=180∘
4. Substituting the Known Value:
- We know ∠AOB=115∘, so we can substitute this into the equation:
115∘+∠COD=180∘
5. Solving for ∠COD:
- To find ∠COD, we rearrange the equation:
∠COD=180∘−115∘
- Calculating this gives:
∠COD=65∘
Final Answer:
∠COD=65∘
- We have a quadrilateral ABCD with an inscribed circle centered at point O.
- The circle touches all four sides of the quadrilateral.
- We are given that ∠AOB=115∘.
- By the properties of a cyclic quadrilateral (or a quadrilateral with an inscribed circle), the angles at the center formed by the diagonals are related to the angles at the vertices.
- The angles at the center O corresponding to opposite sides of the quadrilateral are supplementary. This means:
∠AOB+∠COD=180∘
- We know ∠AOB=115∘, so we can substitute this into the equation:
115∘+∠COD=180∘
- To find ∠COD, we rearrange the equation:
∠COD=180∘−115∘
- Calculating this gives:
∠COD=65∘
∠COD=65∘
Topper's Solved these Questions
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE48videos
QUADRILATERAL
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions200videos
PROFIT & LOSS
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS113videos
RATIO & PROPORTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Choose the quadrilateral in which all the four sides are not equal.
ARhombusBSquareCRectangleDNone of these - Question 2 - Select One
A circle touches a quadrilateral ABCD. Find the true statement:
 AAB+BC=CD+ADBAB+CD=BC+ADCBD=ACDnone of the above
AAB+BC=CD+ADBAB+CD=BC+ADCBD=ACDnone of the above
Write converse, inverse and contraposilive of the implication: if a quadrilatera ABCD is a square, all the sides of the quadrilateral ABCD are equal.
View SolutionA circle touches all the four sides of a quadrilateral ABCD . Prove that: AB+CD=BC+DA .
View SolutionIn the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :
 View Solution
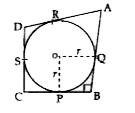
View SolutionIn the following figure ,a circle with centre O is inscribed in a quadrilateral ABCD such that ,it touches the sides BC, AB, AD and CD at points P,Q , R and S respectively .If AB =29 cm , AD =23 cm ∠B=90∘andDS=5 cm.
Find the value of DR :
 View Solution
View SolutionIn Fig. 2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB=29 cm, AD-23 cm,∠B=90° and DS = 5 cm, then the radius of the circle (in cm)
View SolutionIn Fig the quadrilateral ABCD circumscribes a circle with centre O. If ∠AOB=115∘, then find ∠AOB=115∘ then find ∠COD.
 View Solution
View Solution

