A circle touches all sides of quadrilateral ABCD then which one of these is true :
AB+BC=CD+DA
AB+AD=BC+CD
AB+CD=BC+DA
AB+BC+CD+DA=4× diameter of circle
To solve the problem, we need to analyze the properties of a quadrilateral ABCD that has an inscribed circle (also known as a tangential quadrilateral). The key property of such quadrilaterals is that the sum of the lengths of the opposite sides is equal.
1. Understanding the Problem:
- We have a quadrilateral ABCD with a circle that touches all its sides. This means that the quadrilateral is tangential.
2. Using the Property of Tangential Quadrilaterals:
- For a tangential quadrilateral, the following relationship holds:
AB+CD=AD+BC
- This means that the sum of the lengths of one pair of opposite sides is equal to the sum of the lengths of the other pair of opposite sides.
3. Identifying the Correct Option:
- Given the options, we need to identify which one states that AB+CD=AD+BC.
- According to our understanding, this is a true statement for any tangential quadrilateral.
4. Conclusion:
- Therefore, the correct answer is that AB+CD=AD+BC is true.
- We have a quadrilateral ABCD with a circle that touches all its sides. This means that the quadrilateral is tangential.
- For a tangential quadrilateral, the following relationship holds:
AB+CD=AD+BC
- This means that the sum of the lengths of one pair of opposite sides is equal to the sum of the lengths of the other pair of opposite sides.
- Given the options, we need to identify which one states that AB+CD=AD+BC.
- According to our understanding, this is a true statement for any tangential quadrilateral.
- Therefore, the correct answer is that AB+CD=AD+BC is true.
Topper's Solved these Questions
Similar Questions
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
View SolutionIn the given figure, a circle touches the sides of the quadrilateral PQRS. The radius of the circle is 9cm. ∠RSP=∠SRQ=60∘and∠PQR=∠QPS=120∘. What is the perimeter (in cm) of the quadrilateral?
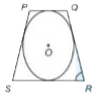
View Solution
Knowledge Check
In the figure, a circle touches all the four sides of a quadrilateral ABCD whose sides AB= 6.5 cm, BD= 5.4 cm and CD = 5.3 cm . The length of AC is :
 A4.6 cmB5.8 cmC6.2 cmD6.4 cm
A4.6 cmB5.8 cmC6.2 cmD6.4 cmA circle touches a quadrilateral ABCD. Find the true statement:
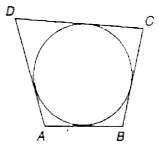 AAB+BC=CD+ADBAB+CD=BC+ADCBD=ACDnone of the above
AAB+BC=CD+ADBAB+CD=BC+ADCBD=ACDnone of the aboveA circle touches the sides of a quadrilateral ABCD at P, Q, R and S respectively. Find the angles subtended at the centre by a pair of opposite sides.
A180∘B270∘C225∘DNone of these
A circle touches all the four sides of a quadrilateral ABCD . Prove that: AB+CD=BC+DA .
View SolutionA circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.
View SolutionA circle touches all the four sides of a quadrilateral ABCD. If AB = 9 cm, BC= 8 cm and CD = 12 cm, then what is DA equal to?
View SolutionIf circle touches all the sides of a quadrilateral ABCD, if AB = 7 cm, CD = 3 cm, BC = 8.5 cm. Find the length of AD.
View Solution
