A thermal conductor is heated at one end. What is the theoretical value of its thermal conductivity in order that the other end also attains the same temperature?
To solve the problem of finding the theoretical value of thermal conductivity for a thermal conductor heated at one end such that the other end also attains the same temperature, we can follow these steps:
1. Understanding Thermal Conductivity:
- Thermal conductivity (K) is a measure of a material's ability to conduct heat. It is defined by the equation:
K=Q⋅LA⋅ΔT⋅t
where Q is the heat transferred, L is the length of the conductor, A is the cross-sectional area, ΔT is the temperature difference across the conductor, and t is the time.
2. Setting Up the Problem:
- In this scenario, one end of the thermal conductor is heated to a temperature T, and we want the other end to also reach the same temperature T. This means that the temperature difference ΔT across the conductor must be zero.
3. Analyzing the Condition:
- If the temperature difference ΔT=Thot−Tcold=0, then:
ΔT=0
- This implies that the temperature at both ends of the conductor is equal.
4. Implications for Thermal Conductivity:
- From the formula for thermal conductivity, if ΔT approaches zero, the equation suggests that the thermal conductivity K must approach infinity to maintain a finite heat transfer rate Q. This is because if K were finite, then a zero temperature difference would imply no heat transfer, contradicting the condition that both ends are at the same temperature.
5. Conclusion:
- Therefore, for the other end of the thermal conductor to attain the same temperature as the heated end, the theoretical value of thermal conductivity must be infinite:
K=∞
Final Answer:
The theoretical value of thermal conductivity required for the other end of the thermal conductor to attain the same temperature is K=∞.
---
- Thermal conductivity (K) is a measure of a material's ability to conduct heat. It is defined by the equation:
K=Q⋅LA⋅ΔT⋅t
where Q is the heat transferred, L is the length of the conductor, A is the cross-sectional area, ΔT is the temperature difference across the conductor, and t is the time.
- In this scenario, one end of the thermal conductor is heated to a temperature T, and we want the other end to also reach the same temperature T. This means that the temperature difference ΔT across the conductor must be zero.
- If the temperature difference ΔT=Thot−Tcold=0, then:
ΔT=0
- This implies that the temperature at both ends of the conductor is equal.
- From the formula for thermal conductivity, if ΔT approaches zero, the equation suggests that the thermal conductivity K must approach infinity to maintain a finite heat transfer rate Q. This is because if K were finite, then a zero temperature difference would imply no heat transfer, contradicting the condition that both ends are at the same temperature.
- Therefore, for the other end of the thermal conductor to attain the same temperature as the heated end, the theoretical value of thermal conductivity must be infinite:
K=∞
The theoretical value of thermal conductivity required for the other end of the thermal conductor to attain the same temperature is K=∞.
Topper's Solved these Questions
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:LONG ANSWER QUESTIONS
Explore 5 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SHORT ANSWER QUESTIONS
Explore 19 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K
Explore 2 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
- THERMAL RADIATION Book:ICSEChapter:THERMAL RADIATION Exercise:SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
Explore 14 Videos
Similar Questions
Which of the following cylindrical rods will conduct most heat, when their ends are maintained at the same steady temperature
View SolutionTwo rectangular blocks A and B of different metals have same length and same area of cross-section. They are kept in such a way that their cross-sectional area touch each other. The temperature at one end of A is 100∘C and B at the other end is 0∘C. If the ratio of their thermal conductivity is 1:3, then under steady state, the temperature of the junction in contact will be
View SolutionTwo plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View SolutionA long rod has one end at 0∘C and other end at a high temperature. The coefficient of thermal conductivity varies with distance from the low temperature end as K=K0(1+ax), where K0=102 SI unit and a=1m−1 . At what distance from the first end the temperature will be 100∘C? The area of cross-section is 1cm2 and rate of heat conduction is 1 W.
View SolutionTwo rectangular blocks, having identical dimensions, an be arranged either in configuration-I or in configuration-II as shown in the figure. One of the blocks has thermal conductivity k and the other 2k. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9s to transport a certain amount of heat from the hot end to the cold end in the configuration-I. The time to transport the same amount of heat in the configuration-II is
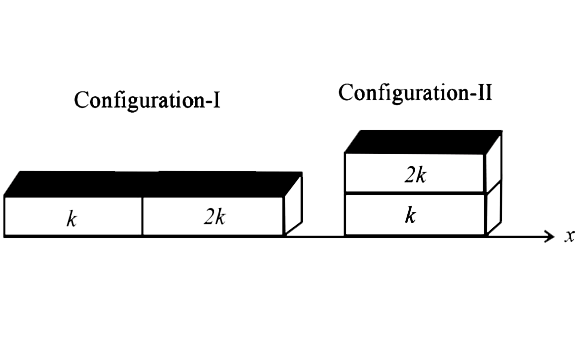
View SolutionTwo rectangular blocks, having identical dimensions, an be arranged either in configuration-I or in configuration-II as shown in the figure. One of the blocks has thermal conductivity k and the other 2k. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9s to transport a certain amount of heat from the hot end to the cold end in the configuration-I. The time to transport the same amount of heat in the configuration-II is

View SolutionRate of heat flow through two conducting rods of identical dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View SolutionThe area of cross-section of rod is given by A=A0(1+αx) where A0 & α are constant and x is the distance from one end. If the thermal conductivity of the material is K. What is the thermal resistancy of the rod if its length is l0?
View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
View Solution
