In a hostel of 100 students capacity 42 are science graduate 34 are law graduate and 58 are commerce graduate. 8 students are science and law graduate,. 13 students are law and commerce graduate 18 students are commerce and science graduate. How many student are only science graduate?
To find the number of students who are only science graduates, we can use the principle of inclusion-exclusion and a Venn diagram approach. Let's break it down step by step.
Step 1: Define the Sets
Let:
- S = Set of Science graduates
- L = Set of Law graduates
- C = Set of Commerce graduates
From the problem, we have:
- |S|=42 (Total Science graduates)
- |L|=34 (Total Law graduates)
- |C|=58 (Total Commerce graduates)
- |S∩L|=8 (Students who are both Science and Law graduates)
- |L∩C|=13 (Students who are both Law and Commerce graduates)
- |C∩S|=18 (Students who are both Commerce and Science graduates)
Step 2: Find the Number of Students in Each Intersection
We need to find the number of students who are only Science graduates. To do this, we need to account for those who are also in the other categories.
Let:
- x = Students who are only Science graduates
- y = Students who are only Law graduates
- z = Students who are only Commerce graduates
From the intersections, we can express the total number of Science graduates as:
|S|=x+(|S∩L|)+(|C∩S|)−(|S∩L∩C|)
Where |S∩L∩C| is the number of students who are graduates in all three fields. However, we do not have this value directly.
Step 3: Use the Inclusion-Exclusion Principle
Using the information provided, we can set up the equation for Science graduates:
42=x+8+18−z
Where z is the number of students who are in all three categories.
Step 4: Find the Total Students
We also know that the total number of students is 100. Therefore, we can express the total number of students as:
100=x+y+z+(|S∩L|)+(|L∩C|)+(|C∩S|)−2(|S∩L∩C|)
However, we will focus on finding x directly.
Step 5: Calculate Only Science Graduates
From the previous equation:
42=x+8+18−z
Rearranging gives:
x=42−8−18+z
x=16+z
Step 6: Determine the Value of z
Since we do not have the exact number of students who are graduates in all three fields, we can assume that z=0 for the calculation of only Science graduates. This gives:
x=16+0=16
Conclusion
Thus, the number of students who are only Science graduates is:
16
Let:
- S = Set of Science graduates
- L = Set of Law graduates
- C = Set of Commerce graduates
- |S|=42 (Total Science graduates)
- |L|=34 (Total Law graduates)
- |C|=58 (Total Commerce graduates)
- |S∩L|=8 (Students who are both Science and Law graduates)
- |L∩C|=13 (Students who are both Law and Commerce graduates)
- |C∩S|=18 (Students who are both Commerce and Science graduates)
We need to find the number of students who are only Science graduates. To do this, we need to account for those who are also in the other categories.
- x = Students who are only Science graduates
- y = Students who are only Law graduates
- z = Students who are only Commerce graduates
|S|=x+(|S∩L|)+(|C∩S|)−(|S∩L∩C|)
Where |S∩L∩C| is the number of students who are graduates in all three fields. However, we do not have this value directly.
Using the information provided, we can set up the equation for Science graduates:
42=x+8+18−z
Where z is the number of students who are in all three categories.
We also know that the total number of students is 100. Therefore, we can express the total number of students as:
100=x+y+z+(|S∩L|)+(|L∩C|)+(|C∩S|)−2(|S∩L∩C|)
However, we will focus on finding x directly.
From the previous equation:
42=x+8+18−z
Rearranging gives:
x=42−8−18+z
x=16+z
Since we do not have the exact number of students who are graduates in all three fields, we can assume that z=0 for the calculation of only Science graduates. This gives:
x=16+0=16
Thus, the number of students who are only Science graduates is:
16
Topper's Solved these Questions
Similar Questions
In a hostel of 100 students capacity 42 are science graduate 34 are law graduate and 58 are commerce graduate. 8 students are science and law graduate,. 13 students are law and commerce graduate 18 students are commerce and science graduate. How many student are only science graduate?
View SolutionThe given Venn diagram shows the number of students who have passed in the three exams, viz, english, science and Maths. How many students failed in all the three exams?
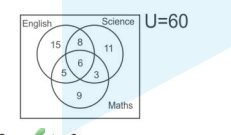
View Solution
Knowledge Check
Out of 450 students in a school , 193 students read Science Today , 200 students read Science Refresher, while 80 students read neither. How many students read both the magazines ?
A137B80C57D23In a college 40% students are graduates. If the number of graduates is 7000, then what are the total number of students in the college?
A19500B18000C17500D21500Different choices made by a group of 200 students are given below in percentage. The number of students who have taken neither Science and Commerce is
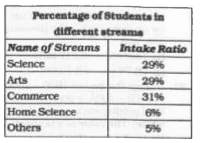 A80B120C60D40
A80B120C60D40
In a class, 15% of total number of students failed in Science, 25% of total number of students failed in Maths and 10% of total number of students failed in both. How much percentage of students passed in both Maths and Science?
View SolutionIn a class of 55 students, 40 like Science and 29 like Mathematics. If each student likes at least one subject, answer the following questions.
How many like only Science?
View SolutionIn a class, there are 80 students who study both Computer Science and Electronics. While 100 students study Computer Science, 120 students study Electronics. How many of them study Computer Science only?
View SolutionIn a class of 55 students. 40 like Science and 29 like Mathematics. If each student likes at least one subject, answer the following questions.
How many like both Science and Mathematics?
View SolutionIn the Venn diagram shown here, the triangle represents students the circle represents diploma holders and the quadrilateral represents graduates. The number given in the diagram represents number of persons of that particular category.
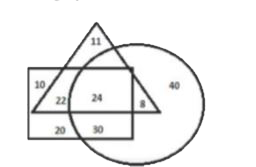
How many students are diploma holders but NOT graduates?
View Solution
