Question

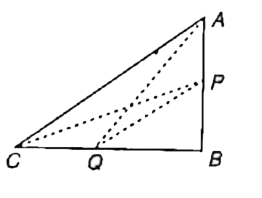
In an isosceles right angle triangle ABC (at B) perpendicular are drawn from a point D inside the triangle on side AB and AC meet at p and Q respectively . AP = a unit ,AQ = b unit $\angle$PAD = ${15}^{\circ }$, sin 75° = ?

Options

A. (a) 2b/√3a
B. (b) a/2b
C. (c) √3a/2b
D. (d) 2a/√3b

Answer

`(sqrt(3) a)/( 2 b )`

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Triangle Configuration
We have an isosceles right triangle ABC with a right angle at B. Points P and Q are where perpendiculars from point D (inside the triangle) meet sides AB and AC, respectively. We know AP = a units, AQ = b units, and angle PAD = 15°.

Step 2: Determine Angle Relationships
Since triangle ABC is a right triangle at B, the angles at A and C are both 45°. We can find angle ADQ using the angle sum property:
- Angle PAD = 15°
- Angle ADB = 90° (since it’s a right triangle)
- Therefore, angle ADQ = 90° - 15° = 75°.

Step 3: Use the Sine Definition
To find sin 75°, we can use the definition of sine in triangle ADQ:
- sin(75°) = Opposite side (AQ) / Hypotenuse (AD).

Step 4: Express AD in Terms of a and b
In triangle ADQ, we can apply the sine function:
- sin(60°) = Opposite (AQ) / Hypotenuse (AD)
- We know AQ = b, and sin(60°) = √3/2.

Thus, we can set up the equation:
\( \sin(60°) = \frac{b}{AD} \)
\( \frac{\sqrt{3}}{2} = \frac{b}{AD} \)
From this, we can solve for AD:
\( AD = \frac{2b}{\sqrt{3}} \)

Step 5: Substitute AD into the sin(75°) Equation
Now we can substitute AD back into the equation for sin(75°):
\( \sin(75°) = \frac{AP}{AD} = \frac{a}{\frac{2b}{\sqrt{3}}} \)
This simplifies to:
\( \sin(75°) = \frac{a \cdot \sqrt{3}}{2b} \)

Final Answer
Thus, the value of sin 75° in terms of a and b is:
\( \sin(75°) = \frac{\sqrt{3}a}{2b} \)

---