A block is released from A on a frictionless track as shown in Fig. 7.2.6. What is the magnitude of radial acceleration and the total acceleration of the block at B ?
Let AC = H= 7 m, Radius of the curved portion = r = 3 m
Decrease in P.E. of the block in reaching B = Increase in its K.E.
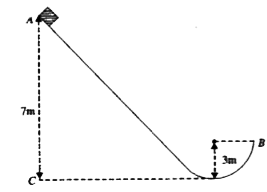
mg(H−r)=12mv2
v2=g(H−r)
Radial acceleration =v2r=g(H−r)r
ar=9.8(7−3)3=13.1m/s2
Tangential acceleration =at=9.8m/s2
Total acceleration =a= ?
a=√a2r+a2t
=√13.12+9.82
=16.36m/s2
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )11videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)8videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
Similar Questions
In the figure shown acceleration of the block is
 View Solution
View SolutionIn the setup shown, fird acceleration of the block C.
 View Solution
View Solution34.The magnitude of acceleration of blocks of mass
View SolutionIf block B moves towards right with acceleration b, find the net acceleration of block A.
 View Solution
View SolutionA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
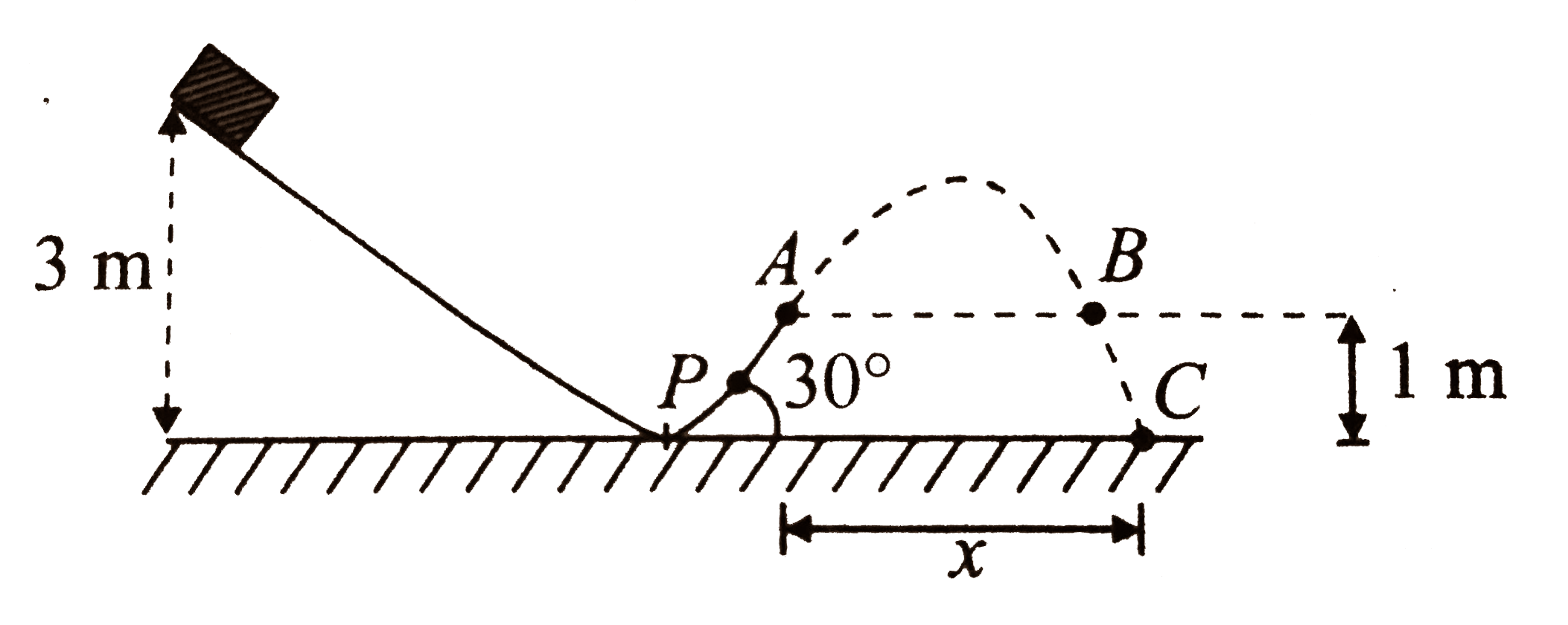 .
.
The time taken by the block to move from A to B is.View SolutionA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
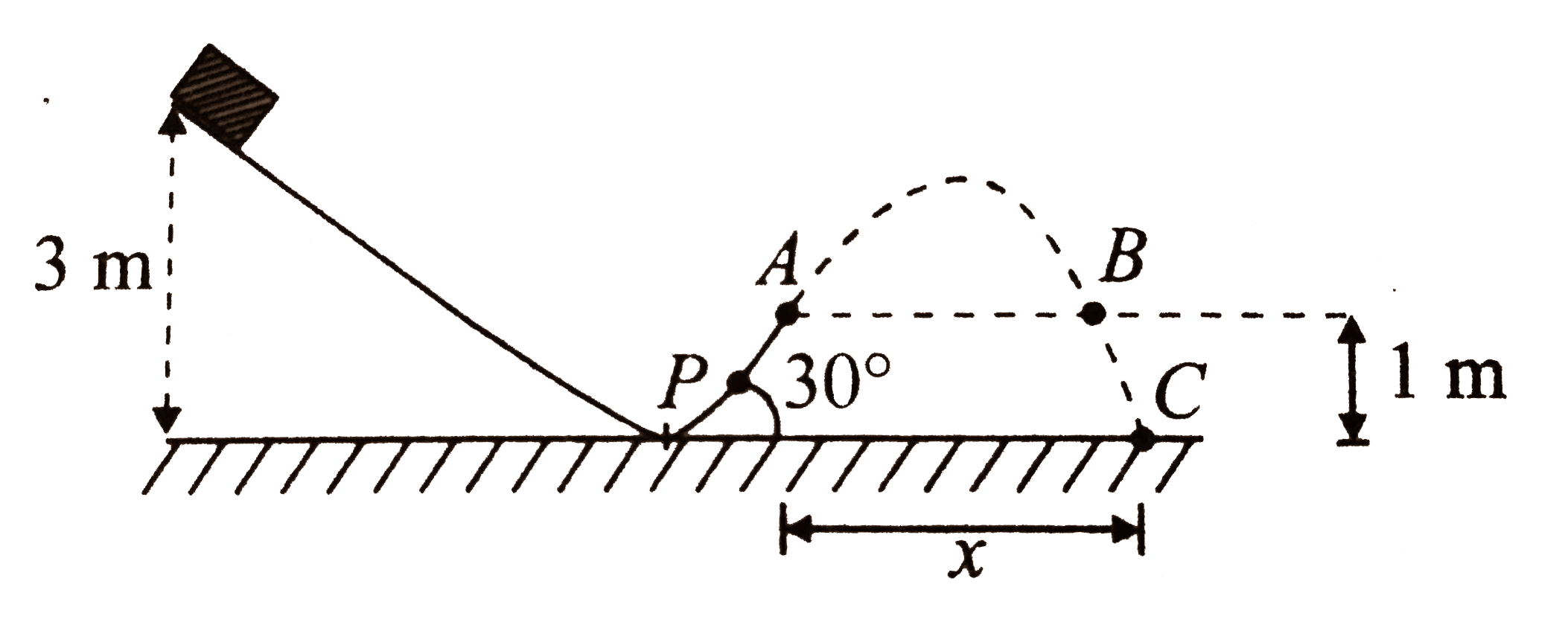 .
.
The time taken by the block to move from A to C is.View SolutionA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
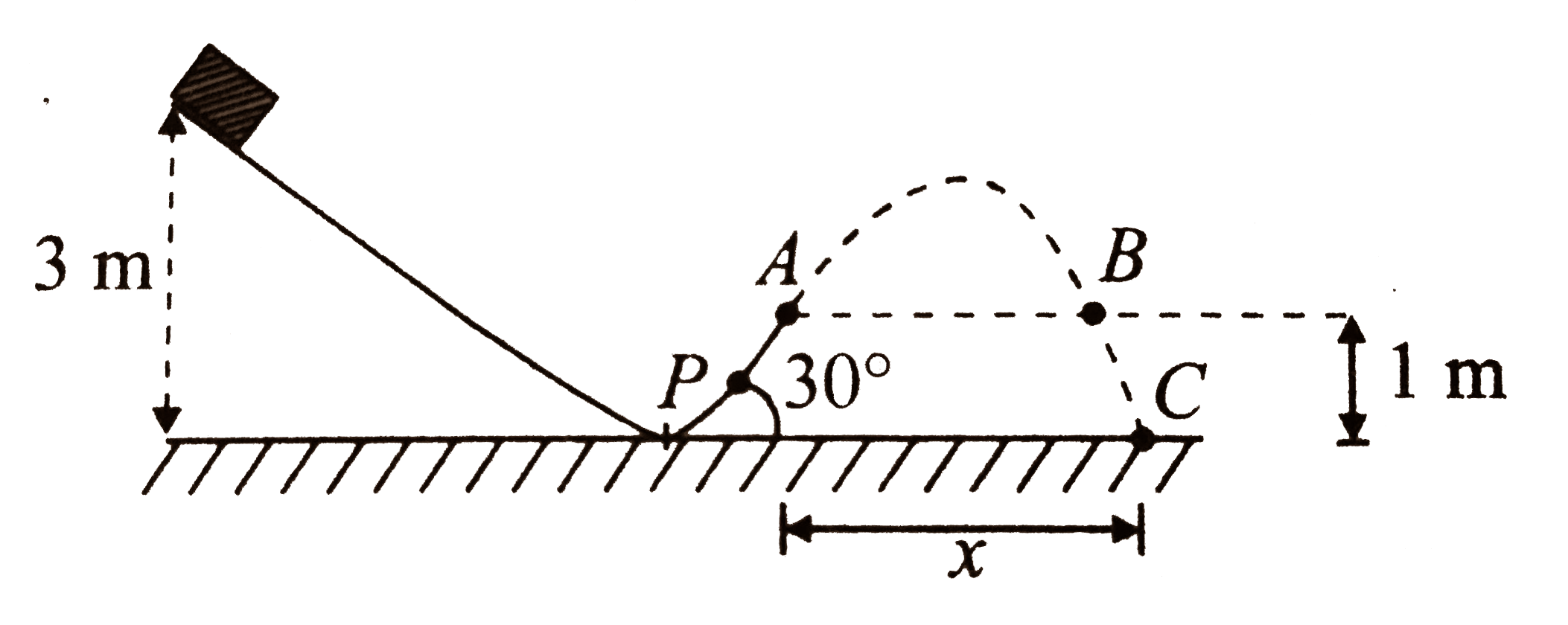 .
.
The horizontal distance x travelled by the block in moving from A to C is.View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 View Solution
View SolutionA block of mass m slides along a frictionless surface as shown in the figure. If it is releases from rest from A what is its speed at B?
 View Solution
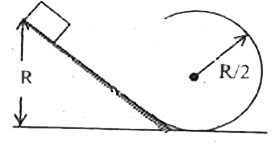
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
 View Solution
View Solution

