A long non-conducting, massless rod of length L pivoted at its centre and balanced with a weight w at a distance x from the lefrt end. At the left and right ends fo the rod are attached small conducting sphers with positive charfges q and 2q respectively. A distance h directly beneath each of these spheres is a fixed sphere with positive charge Q.
(a) Find the distance x where the rod is horizontal and balanced.b. What valueshold h have so that the rod exerts no vertical force on the bearing when the rod is horizontal and balanced?
The correct Answer is:B, C, D
To solve the problem step by step, we will analyze the forces and torques acting on the rod and derive the necessary equations.
Step 1: Understanding the Setup
We have a long non-conducting massless rod of length L pivoted at its center. A weight W is placed at a distance x from the left end. At the ends of the rod, there are small conducting spheres with charges q and 2q respectively. Below these spheres, at a distance h, there are fixed spheres with charge Q.
Step 2: Analyzing the Torques
For the rod to be horizontal and balanced, the net torque about the pivot must be zero. The torques due to the weight W and the electrostatic forces from the charges must balance each other.
1. Torque due to weight W:
- The distance from the pivot to the weight is L2−x.
- Torque due to weight W is given by:
τW=W(L2−x)
2. Torque due to electrostatic forces:
- The force between the charge q (left end) and charge Q (below it) is:
F1=14πϵ0qQh2
- The torque due to this force about the pivot is:
τF1=F1(L2)=14πϵ0qQh2⋅L2
- The force between charge 2q (right end) and charge Q (below it) is:
F2=14πϵ02qQh2
- The torque due to this force about the pivot is:
τF2=F2(L2)=14πϵ02qQh2⋅L2
Step 3: Setting Up the Equation for Balance
Setting the total torque due to the electrostatic forces equal to the torque due to the weight:
W(L2−x)=L2(14πϵ0qQh2+14πϵ02qQh2)
Simplifying this gives:
W(L2−x)=L2⋅3qQ4πϵ0h2
Step 4: Solving for x
Rearranging the equation to solve for x:
W(L2−x)=3LqQ8πϵ0h2
L2−x=3qQ8πϵ0Wh2
x=L2−3qQ8πϵ0Wh2
Step 5: Finding the Value of h for No Vertical Force
For the rod to exert no vertical force on the bearing, the upward electrostatic forces must equal the downward weight:
W=3qQ4πϵ0h2
Rearranging gives:
h2=3qQ4πϵ0W
Taking the square root:
h=√3qQ4πϵ0W
Final Answers
(a) The distance x where the rod is horizontal and balanced is:
x=L2−3qQ8πϵ0Wh2
(b) The value of h such that the rod exerts no vertical force on the bearing is:
h=√3qQ4πϵ0W
We have a long non-conducting massless rod of length L pivoted at its center. A weight W is placed at a distance x from the left end. At the ends of the rod, there are small conducting spheres with charges q and 2q respectively. Below these spheres, at a distance h, there are fixed spheres with charge Q.
For the rod to be horizontal and balanced, the net torque about the pivot must be zero. The torques due to the weight W and the electrostatic forces from the charges must balance each other.
- The distance from the pivot to the weight is L2−x.
- Torque due to weight W is given by:
τW=W(L2−x)
- The force between the charge q (left end) and charge Q (below it) is:
F1=14πϵ0qQh2
- The torque due to this force about the pivot is:
τF1=F1(L2)=14πϵ0qQh2⋅L2
F2=14πϵ02qQh2
- The torque due to this force about the pivot is:
τF2=F2(L2)=14πϵ02qQh2⋅L2
Setting the total torque due to the electrostatic forces equal to the torque due to the weight:
W(L2−x)=L2(14πϵ0qQh2+14πϵ02qQh2)
Simplifying this gives:
W(L2−x)=L2⋅3qQ4πϵ0h2
Rearranging the equation to solve for x:
W(L2−x)=3LqQ8πϵ0h2
L2−x=3qQ8πϵ0Wh2
x=L2−3qQ8πϵ0Wh2
For the rod to exert no vertical force on the bearing, the upward electrostatic forces must equal the downward weight:
W=3qQ4πϵ0h2
Rearranging gives:
h2=3qQ4πϵ0W
Taking the square root:
h=√3qQ4πϵ0W
(a) The distance x where the rod is horizontal and balanced is:
x=L2−3qQ8πϵ0Wh2
h=√3qQ4πϵ0W
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
The density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA rod is of length 3 m and its mass acting per unit length is directly proportional to distance x from its one end. The centre of gravity of the rod from that end will be at
View SolutionIn the shown figure, the charge appearing on the conducting shell (grounded) of Radius R, when a point charge q is kept at a distance of d from the centre of the sphere is:

View SolutionTwo identical small conducting spheres having unequal positive charges q1 and q2 are separated by a distance r. If they are now made to touch each other and then separated again to the same distance, the electrostatic force between them in this case will be
View SolutionTwo identical small conducting spheres having unequal positive charges q1 and q2 are separated by a distance r. If they are now made to touch each other and then separated again to the same distance, the electrostatic force between them in this case will be
View SolutionTwo large parallel conducting sheets (placed at finite distance) are given charges Q and 2Q respectively. Find out charges appearing on all the surfaces.
View SolutionThere is a rod of length l , its density varies with length as distance of λ=ax , where x is distance from left end. Find center of mass from left end.
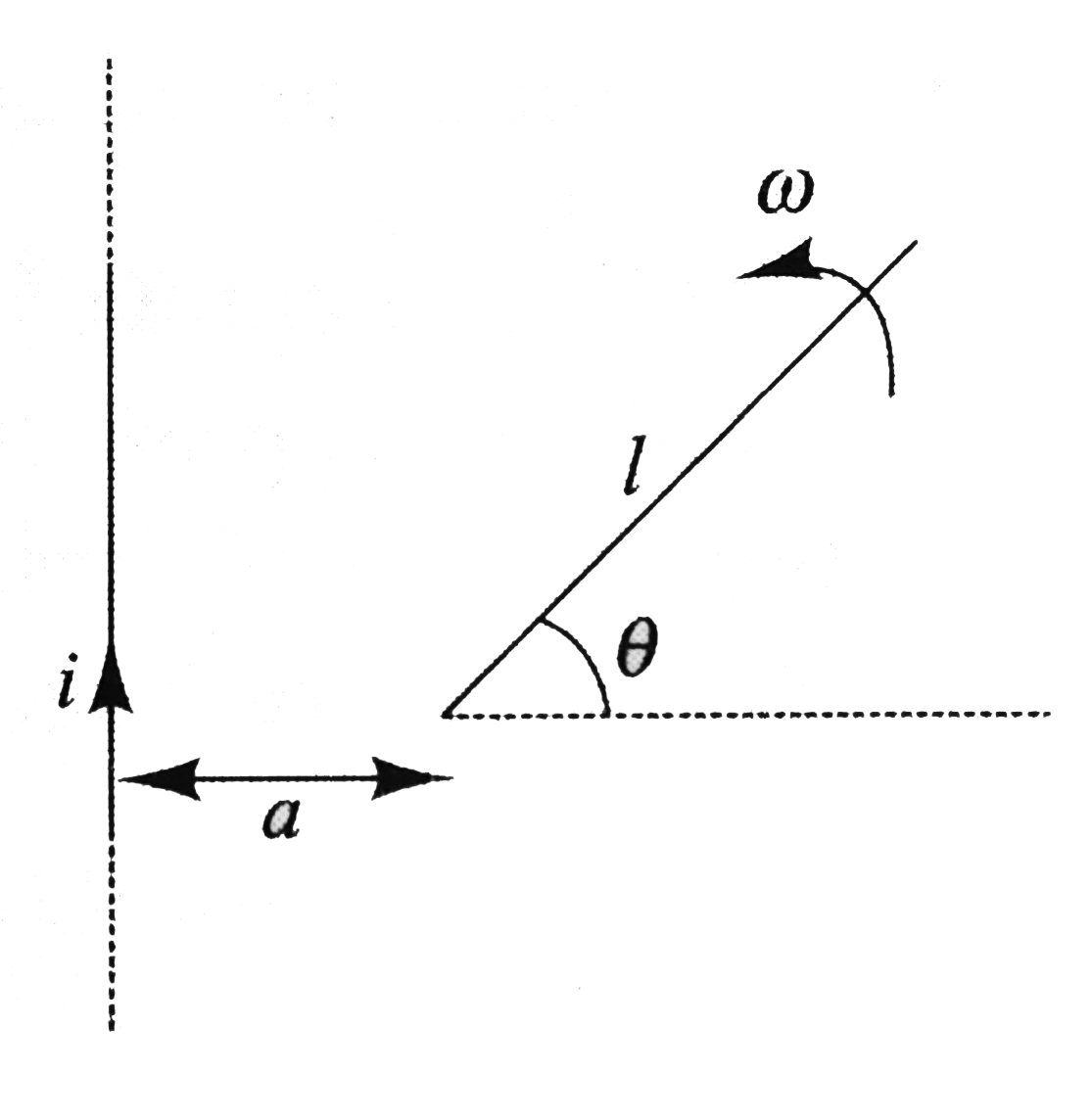
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely long wire carrying current i. Find the emf induced in the rod at the instant shown in .
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
