Question

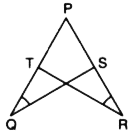
The sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that $\angle PSQ\text{and}\angle PTR$ are right angles
Prove that the triangles PTR and PSQ are congruent.

Explanation

To prove that triangles PTR and PSQ are congruent, we will use the Angle-Side-Angle (ASA) congruence criterion. Here is a step-by-step solution:

Step 1: Identify the given information
We are given that:
- In triangle PQR, sides PQ and PR are equal (PQ = PR).
- Points S and T are on sides PR and PQ, respectively, such that ∠PSQ and ∠PTR are right angles (90 degrees).

Step 2: Draw the triangle and label the points
Draw triangle PQR with points P, Q, and R. Mark points S on PR and T on PQ. Indicate that ∠PSQ and ∠PTR are right angles.

Step 3: State the angles and sides
From the given information, we can state:
1. PQ = PR (given)
2. ∠PSQ = 90° (given)
3. ∠PTR = 90° (given)
4. ∠P is common to both triangles PTR and PSQ.

Step 4: Apply the ASA criterion
Now, we can apply the ASA criterion for triangle congruence:
- We have one angle (∠P) that is common to both triangles.
- We have two sides (PQ and PR) that are equal.
- We have two right angles (∠PSQ and ∠PTR) that are equal.

Step 5: Conclude the proof
Since we have two angles and the included side equal in both triangles, we can conclude that:
Triangle PTR is congruent to triangle PSQ by the Angle-Side-Angle (ASA) criterion.

Thus, we have proved that triangles PTR and PSQ are congruent.