AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
To prove that CD bisects AB, we will follow a step-by-step approach:
Step 1: Draw the Figure
Draw a line segment AB. Mark points A and B on the line segment. From point A, draw a perpendicular line AD such that AD is equal in length to the perpendicular line BC drawn from point B on the opposite side of AB.
Step 2: Label the Points
Label the points as follows:
- A (one end of the line segment)
- B (the other end of the line segment)
- D (the endpoint of the perpendicular from A)
- C (the endpoint of the perpendicular from B)
Step 3: Identify the Intersection Point
Let O be the point where line CD intersects line segment AB.
Step 4: Establish the Given Information
We know:
1. AD = BC (given that they are equal perpendiculars).
2. AD ⊥ AB and BC ⊥ AB (both are perpendicular to AB).
3. Angles AOD and BOC are vertically opposite angles and are equal.
Step 5: Show Triangle Congruence
To prove that AO = BO, we will show that triangles AOD and BOC are congruent.
- Side 1: AD = BC (given).
- Angle 1: Angle AOD = Angle BOC (vertically opposite angles).
- Angle 2: Angle DAO = Angle CBO = 90° (since both AD and BC are perpendicular to AB).
Step 6: Apply the Congruence Criterion
Since we have:
- Two sides equal (AD = BC),
- One angle equal (AOD = BOC),
- One right angle (DAO = CBO),
We can use the Angle-Angle-Side (AAS) criterion for triangle congruence. Thus, we conclude that:
Triangle AOD ≅ Triangle BOC.
Step 7: Conclude with Corresponding Parts
From the congruence of triangles AOD and BOC, we know that the corresponding parts of congruent triangles are equal. Therefore:
AO = BO.
Step 8: Final Conclusion
Since AO = BO, line CD bisects line segment AB.
Draw a line segment AB. Mark points A and B on the line segment. From point A, draw a perpendicular line AD such that AD is equal in length to the perpendicular line BC drawn from point B on the opposite side of AB.
Label the points as follows:
- A (one end of the line segment)
- B (the other end of the line segment)
- D (the endpoint of the perpendicular from A)
- C (the endpoint of the perpendicular from B)
Let O be the point where line CD intersects line segment AB.
We know:
1. AD = BC (given that they are equal perpendiculars).
2. AD ⊥ AB and BC ⊥ AB (both are perpendicular to AB).
3. Angles AOD and BOC are vertically opposite angles and are equal.
To prove that AO = BO, we will show that triangles AOD and BOC are congruent.
- Angle 1: Angle AOD = Angle BOC (vertically opposite angles).
- Angle 2: Angle DAO = Angle CBO = 90° (since both AD and BC are perpendicular to AB).
Since we have:
- Two sides equal (AD = BC),
- One angle equal (AOD = BOC),
- One right angle (DAO = CBO),
Triangle AOD ≅ Triangle BOC.
From the congruence of triangles AOD and BOC, we know that the corresponding parts of congruent triangles are equal. Therefore:
AO = BO.
Since AO = BO, line CD bisects line segment AB.
Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 3 MARKS QUESTIONS
11 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
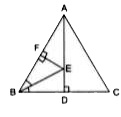
View SolutionIn the following figure , AB = BC , AD ⊥BCandCE⊥AB.prove that AD = CE
View SolutionIn ΔABC,AB=BC,AD⊥BCandCE⊥AB, prove that AD = CE.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View SolutionΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
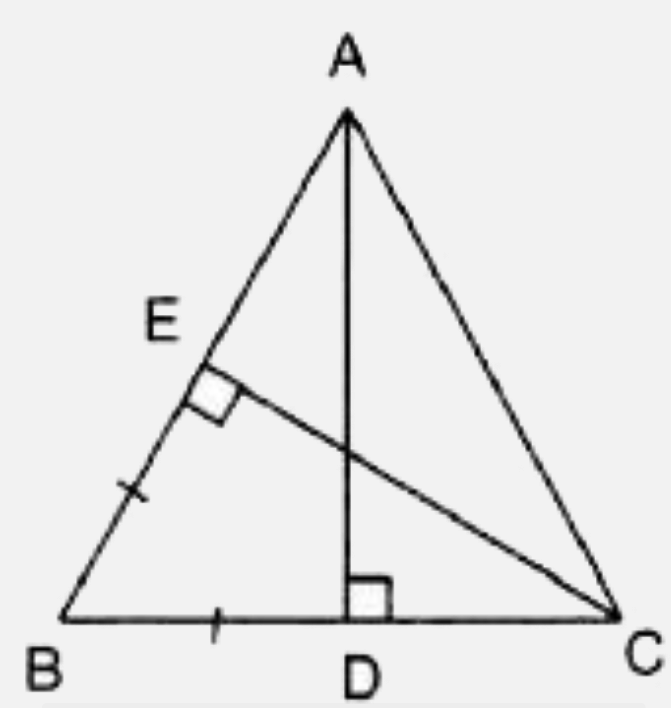
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB. Prove that :
(i) BD = CD
(ii) ED = EF
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View Solution
