AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
17 cm
15 cm
4 cm
8 cm
The correct Answer is:D
To solve the problem step by step, we will follow the reasoning outlined in the video transcript.
Step 1: Identify the Given Information
- Diameter AD = 34 cm
- Chord AB = 30 cm
Step 2: Calculate the Radius of the Circle
The radius (OA) can be calculated as half of the diameter (AD):
OA=AD2=34 cm2=17 cm
Step 3: Bisect the Chord
Since OL is perpendicular to AB and bisects it, we can find the lengths AL and BL:
AL=BL=AB2=30 cm2=15 cm
Step 4: Apply the Pythagorean Theorem
In the right triangle AOL, we can apply the Pythagorean theorem:
OA2=AL2+OL2
Substituting the known values:
172=152+OL2
Step 5: Calculate the Squares
Calculating the squares:
289=225+OL2
Step 6: Solve for OL^2
Rearranging the equation to solve for OL^2:
OL2=289−225
OL2=64
Step 7: Find OL
Taking the square root of both sides:
OL=√64=8 cm
Conclusion
The distance of chord AB from the center of the circle (OL) is 8 cm.
---
- Diameter AD = 34 cm
- Chord AB = 30 cm
The radius (OA) can be calculated as half of the diameter (AD):
OA=AD2=34 cm2=17 cm
Since OL is perpendicular to AB and bisects it, we can find the lengths AL and BL:
AL=BL=AB2=30 cm2=15 cm
In the right triangle AOL, we can apply the Pythagorean theorem:
OA2=AL2+OL2
Substituting the known values:
172=152+OL2
Calculating the squares:
289=225+OL2
Rearranging the equation to solve for OL^2:
OL2=289−225
OL2=64
Taking the square root of both sides:
OL=√64=8 cm
The distance of chord AB from the center of the circle (OL) is 8 cm.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.210videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.320videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
In the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
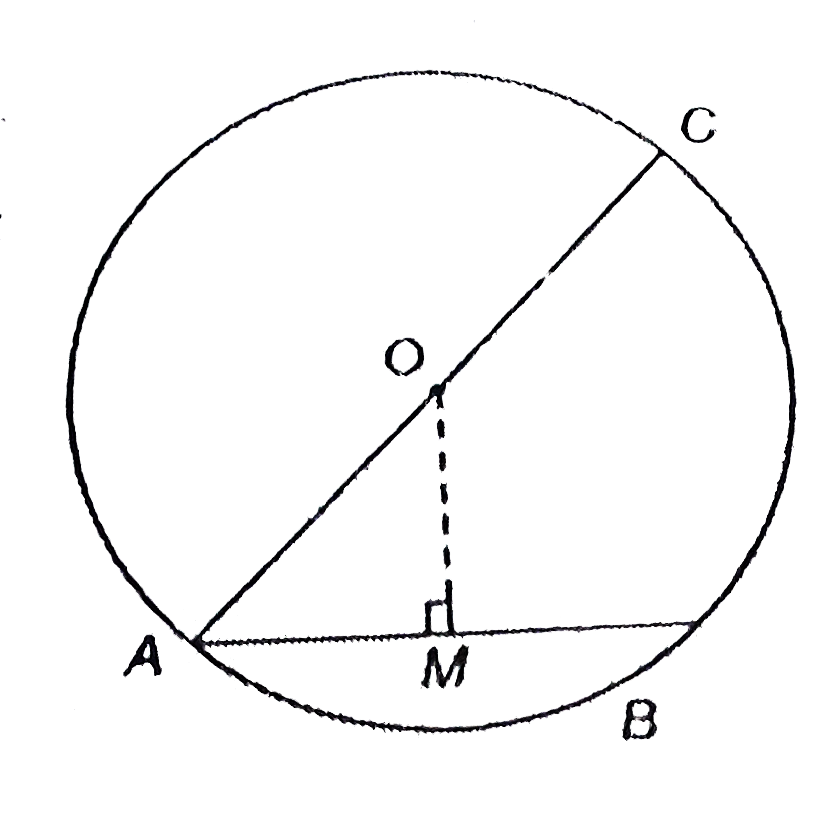 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The diameter of a circle is 34 cm and a chord in that scene circle is 30cm. What is the distance from the center of that circle to the chord ?
A4 cmB8cmC8.5cmD16cm - Question 2 - Select One
In the figure shown , AB is a diameter of the circle and O is the center of the circle If A=(3,4), then what is the circumference of the circle?
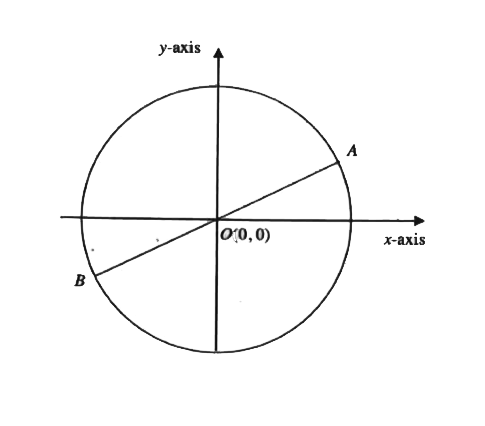 A3B4C4πD10π
A3B4C4πD10π
AB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionIn the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
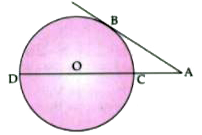 View Solution
View Solution(i) Find the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13cm.
(ii) The length of a chord is 16 cm of a circle of diameter 2 cm. find the perpendicular distance of this chord from the centre of the circle.View SolutionIn the given figure, O is the centre of the circle ans AB is a tangent at B. If AB=15 cm and AC=7.5cm, calculate the radius of the circle.
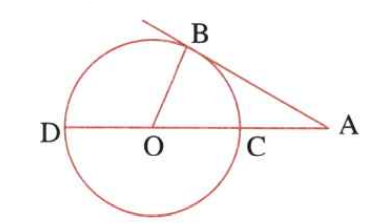 View Solution
View SolutionIf the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is 15 cm (b) 16 cm (c) 17 cm (d) 34 cm
View SolutionA chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
View Solution

