In the following figure, P and Q are the points of intersection of two circles with centres O and O'. If straight lines APB and CQD are parallel to OO', prove that
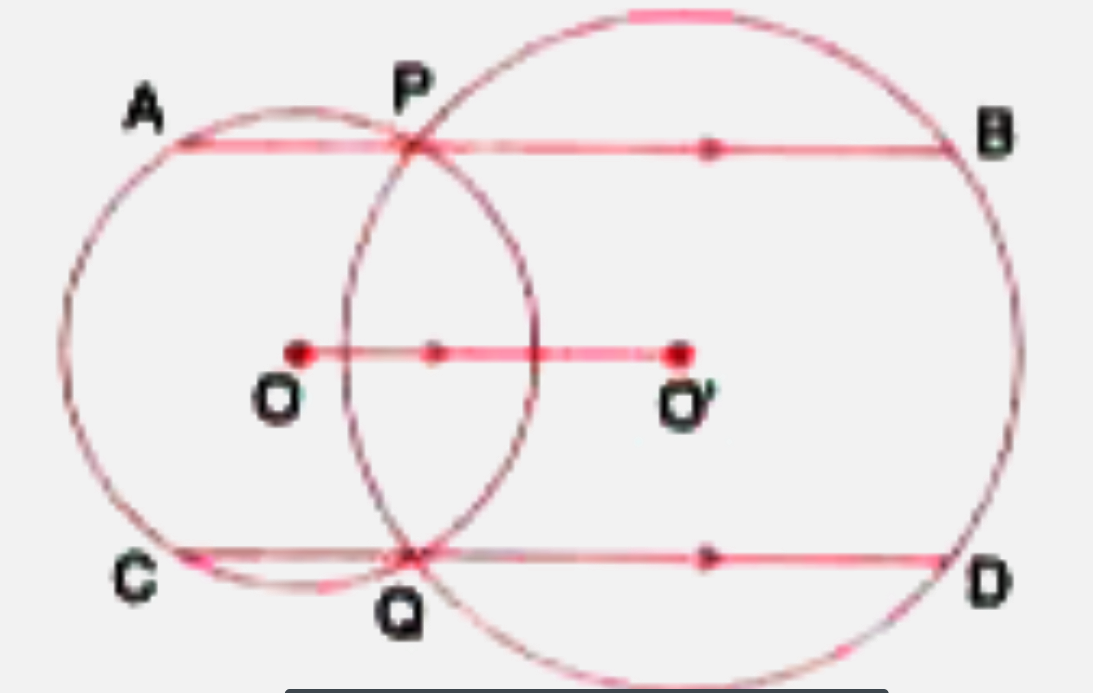
OO'==
Step by step video & image solution for In the following figure, P and Q are the points of intersection of two circles with centres O and O'. If straight lines APB and CQD are parallel to OO', prove that OO'=1/2AB=1/2CD by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(C)29videos
CIRCLE
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)12videos
CIRCLE
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(A)14videos
CIRCLE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA11videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-225videos
CIRCLES
Similar Questions
In Figure, O and O' are centres of two circles intersecting at B and C.ACD is a straight line, find x.
View SolutionIn Figure, P and Q are centres of two circles intersecting at B and C.ACD is a straight line. Then, ∠BQD=
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
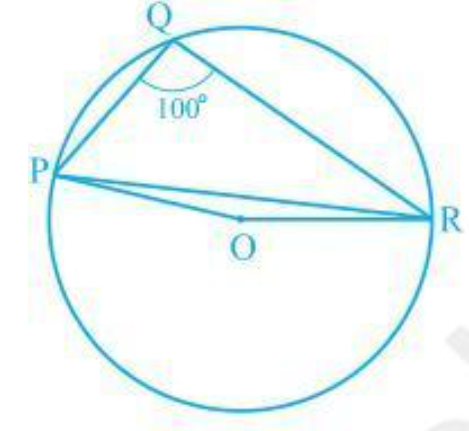 View Solution
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
View SolutionFind the maximum number of points of intersection of 7 straight lines and 5 circles when 3 straight lines are parallel and 2 circle and concentric.
View SolutionFind the maximum number of points of intersection of 7 straight lines and 5 circles when 3 straight lines are parallel and 2 circles are concentric
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
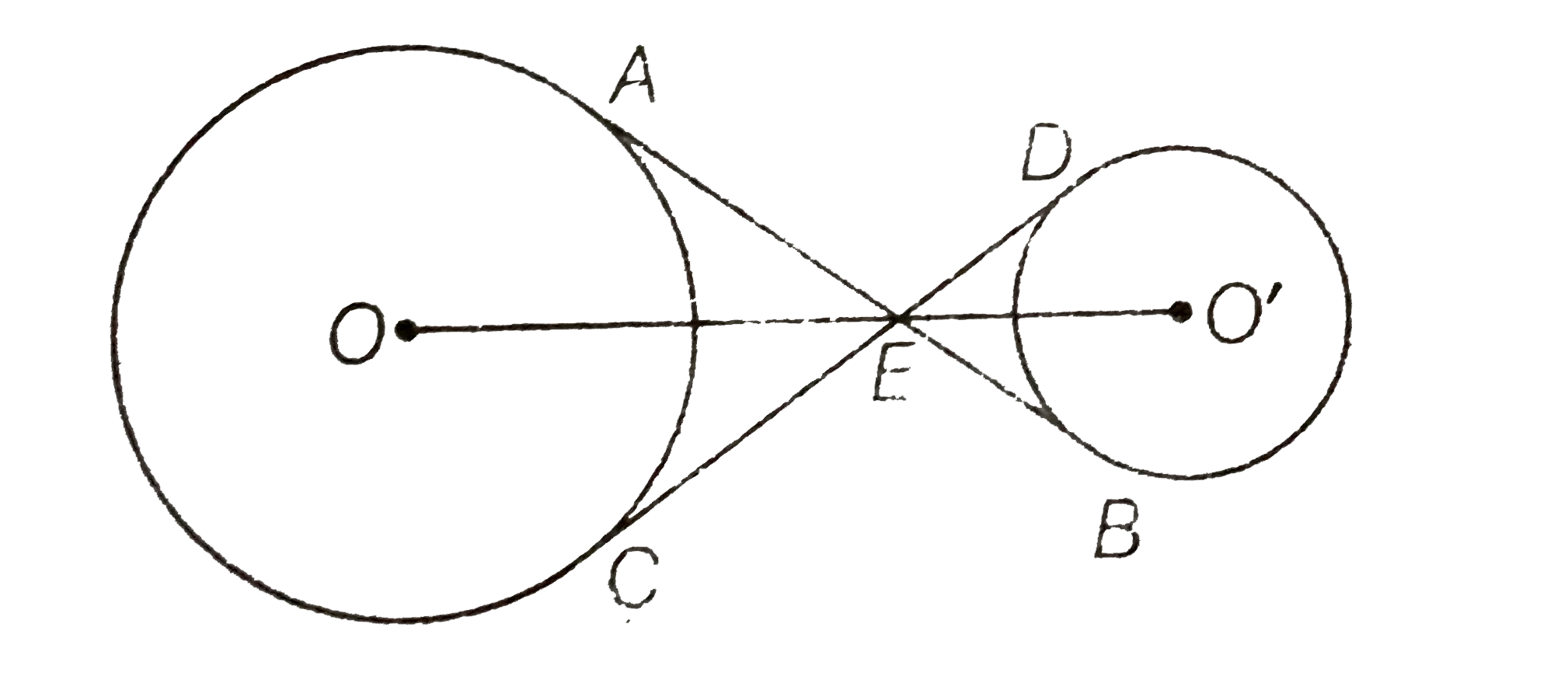 View Solution
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
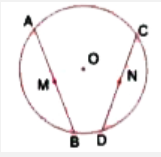
∠AMN=∠CNM.View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
View Solution

