The absolute value function y=f(x)=|x| Draw its graph.
To draw the graph of the absolute value function y=f(x)=|x|, we can follow these steps:
Step 1: Understand the Absolute Value Function
The absolute value function |x| is defined as:
- |x|=x when x≥0
- |x|=−x when x<0
Step 2: Identify Key Points
We can identify key points for the graph:
- When x=0, |0|=0 → Point (0, 0)
- When x=1, |1|=1 → Point (1, 1)
- When x=−1, |−1|=1 → Point (-1, 1)
- When x=2, |2|=2 → Point (2, 2)
- When x=−2, |−2|=2 → Point (-2, 2)
Step 3: Plot the Points
Now, we can plot the identified points on the coordinate system:
- (0, 0)
- (1, 1)
- (-1, 1)
- (2, 2)
- (-2, 2)
Step 4: Draw the Lines
Next, we will connect the points:
1. For x≥0 (right side of the y-axis), the line will be y=x. This is a straight line passing through the origin and extending upwards.
2. For x<0 (left side of the y-axis), the line will be y=−x. This is also a straight line that reflects the right side across the y-axis.
Step 5: Finalize the Graph
The final graph will look like a "V" shape:
- The left arm of the "V" will slope downwards from the point (0, 0) to (-1, 1) and (-2, 2).
- The right arm of the "V" will slope upwards from the point (0, 0) to (1, 1) and (2, 2).
The absolute value function |x| is defined as:
- |x|=x when x≥0
- |x|=−x when x<0
We can identify key points for the graph:
- When x=0, |0|=0 → Point (0, 0)
- When x=1, |1|=1 → Point (1, 1)
- When x=−1, |−1|=1 → Point (-1, 1)
- When x=2, |2|=2 → Point (2, 2)
- When x=−2, |−2|=2 → Point (-2, 2)
Now, we can plot the identified points on the coordinate system:
- (0, 0)
- (1, 1)
- (-1, 1)
- (2, 2)
- (-2, 2)
Next, we will connect the points:
1. For x≥0 (right side of the y-axis), the line will be y=x. This is a straight line passing through the origin and extending upwards.
2. For x<0 (left side of the y-axis), the line will be y=−x. This is also a straight line that reflects the right side across the y-axis.
The final graph will look like a "V" shape:
- The left arm of the "V" will slope downwards from the point (0, 0) to (-1, 1) and (-2, 2).
- The right arm of the "V" will slope upwards from the point (0, 0) to (1, 1) and (2, 2).
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (a)
24 Videos
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (b)
26 Videos
- RELATION AND FUNCTIONSBOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
32 Videos
- SAMPLE QUESTION PAPER 01BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 01EXERCISE - SECTION C
8 Videos
Similar Questions
Describe the real valued function f(x)=ax. Also draw its graph, when 0<a<1.
View SolutionGiven the graph of the function y=f(x), draw the graph of y=sgn(x).
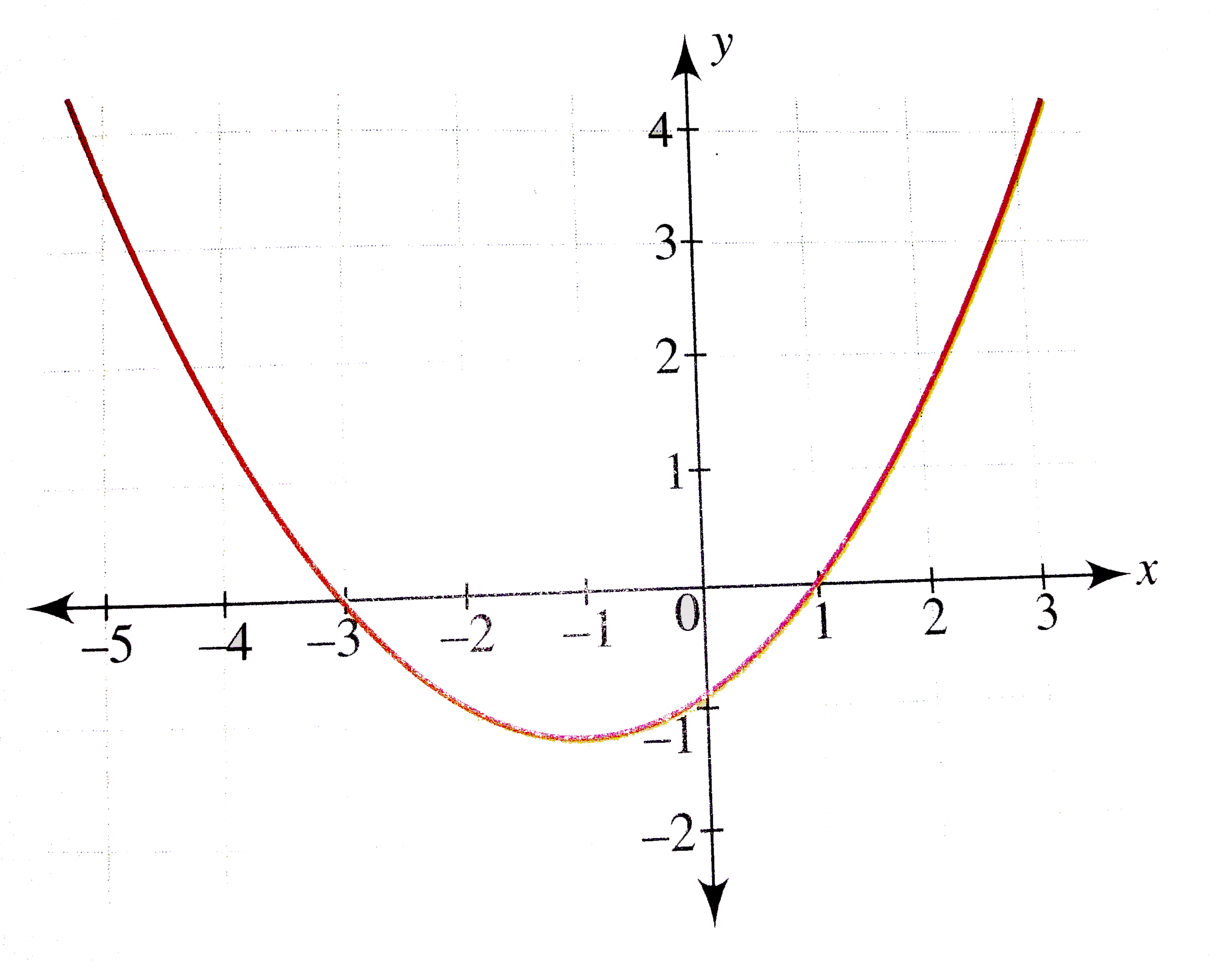
View SolutionDraw the graph of the function f(x)=|x−1|
View SolutionDraw the graph of the function f(x)=−x|x|.
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionDiscuss the maxima and minima of the function f(x)=x23−x43. Draw the graph of y=f(x) and find the range of f(x).
View SolutionDraw the graph of the function: f(x)=log|x|
View SolutionThe graph of the function y=f(x) is as shown in the figure.

Then draw the graphs of
(i) |y|=sgn(f(x)) (ii) |y|=|f(x∣)|
(iii) y=xsgn(f(x))
View SolutionConsider the function f(x)={2x+3,x≤1and−x2+6,x>1} Then draw the graph of the function y=f(x),y=f(|x|)andy=|f(x)|.
View SolutionDraw the graph of the function f(x)=xx
View Solution
