Two cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
To solve the problem, we need to find the relationship between the load resistance R, the internal resistance of the first cell r1, and the internal resistance of the second cell r2 given that the potential difference across the first cell is zero.
1. Understanding the Circuit:
We have two cells (batteries) connected in series, each with an EMF E and internal resistances r1 and r2. They are connected across a load resistance R.
2. Current in the Circuit:
The total EMF in the circuit is the sum of the EMFs of both cells:
Vnet=E+E=2E
The total resistance in the circuit is the sum of the internal resistances and the load resistance:
Rnet=r1+r2+R
Using Ohm's Law, the current I flowing through the circuit can be expressed as:
I=VnetRnet=2Er1+r2+R
3. Potential Difference Across the First Cell:
We are given that the potential difference across the first cell is zero. This means that the voltage drop across the first cell must equal the EMF of the first cell:
VA−VB=0
The potential difference across the first cell can be expressed as:
VA−VB=−E+I⋅r1
Setting this equal to zero gives:
−E+I⋅r1=0⟹E=I⋅r1
4. Substituting for Current:
Substitute the expression for current I into the equation:
E=(2Er1+r2+R)⋅r1
Simplifying this, we can cancel E from both sides (assuming E≠0):
1=2r1r1+r2+R
5. Cross Multiplying:
Cross multiplying gives:
r1+r2+R=2r1
6. Rearranging the Equation:
Rearranging the equation leads to:
r2+R=2r1−r1
Thus:
r2=r1−R
Final Relation:
The final relationship between the load resistance R, the internal resistance of the first cell r1, and the internal resistance of the second cell r2 is:
r2=r1−R
We have two cells (batteries) connected in series, each with an EMF E and internal resistances r1 and r2. They are connected across a load resistance R.
The total EMF in the circuit is the sum of the EMFs of both cells:
Vnet=E+E=2E
The total resistance in the circuit is the sum of the internal resistances and the load resistance:
Rnet=r1+r2+R
Using Ohm's Law, the current I flowing through the circuit can be expressed as:
I=VnetRnet=2Er1+r2+R
We are given that the potential difference across the first cell is zero. This means that the voltage drop across the first cell must equal the EMF of the first cell:
VA−VB=0
The potential difference across the first cell can be expressed as:
VA−VB=−E+I⋅r1
Setting this equal to zero gives:
−E+I⋅r1=0⟹E=I⋅r1
Substitute the expression for current I into the equation:
E=(2Er1+r2+R)⋅r1
Simplifying this, we can cancel E from both sides (assuming E≠0):
1=2r1r1+r2+R
Cross multiplying gives:
r1+r2+R=2r1
Rearranging the equation leads to:
r2+R=2r1−r1
Thus:
r2=r1−R
The final relationship between the load resistance R, the internal resistance of the first cell r1, and the internal resistance of the second cell r2 is:
r2=r1−R
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:Try Yourself
Explore 34 Videos
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
Explore 69 Videos
- COMMUNICATION SYSTEMS Book:AAKASH INSTITUTE ENGLISHChapter:COMMUNICATION SYSTEMS Exercise:ASSIGNMENT SECTION D (Assertion-Reason)
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
Two cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
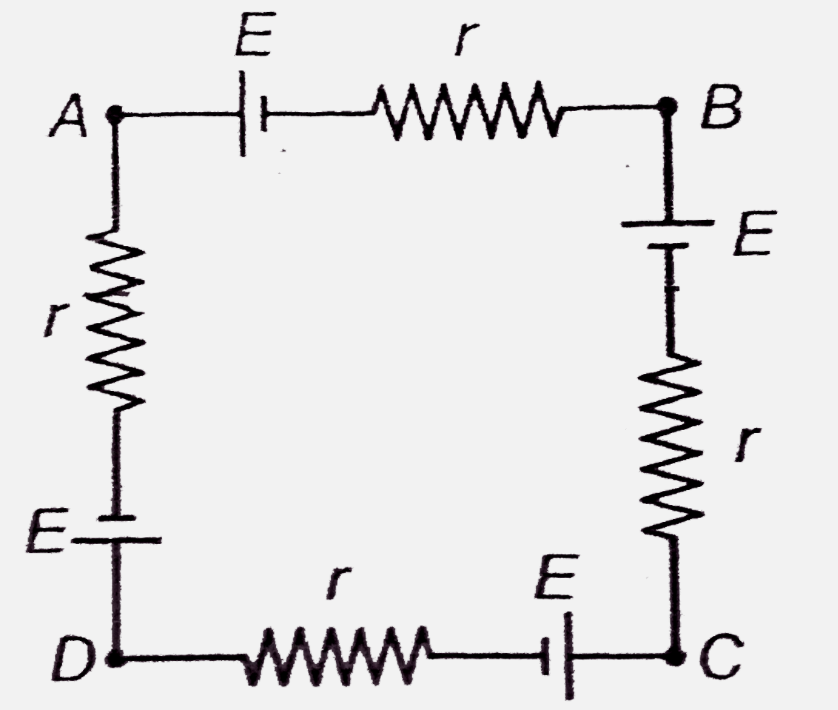
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View Solutionn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionThousand cells of same emf E and same internal resistance r are connected is series in same order without an external resistance . The potential drop across 399 cells is found to be .
View Solution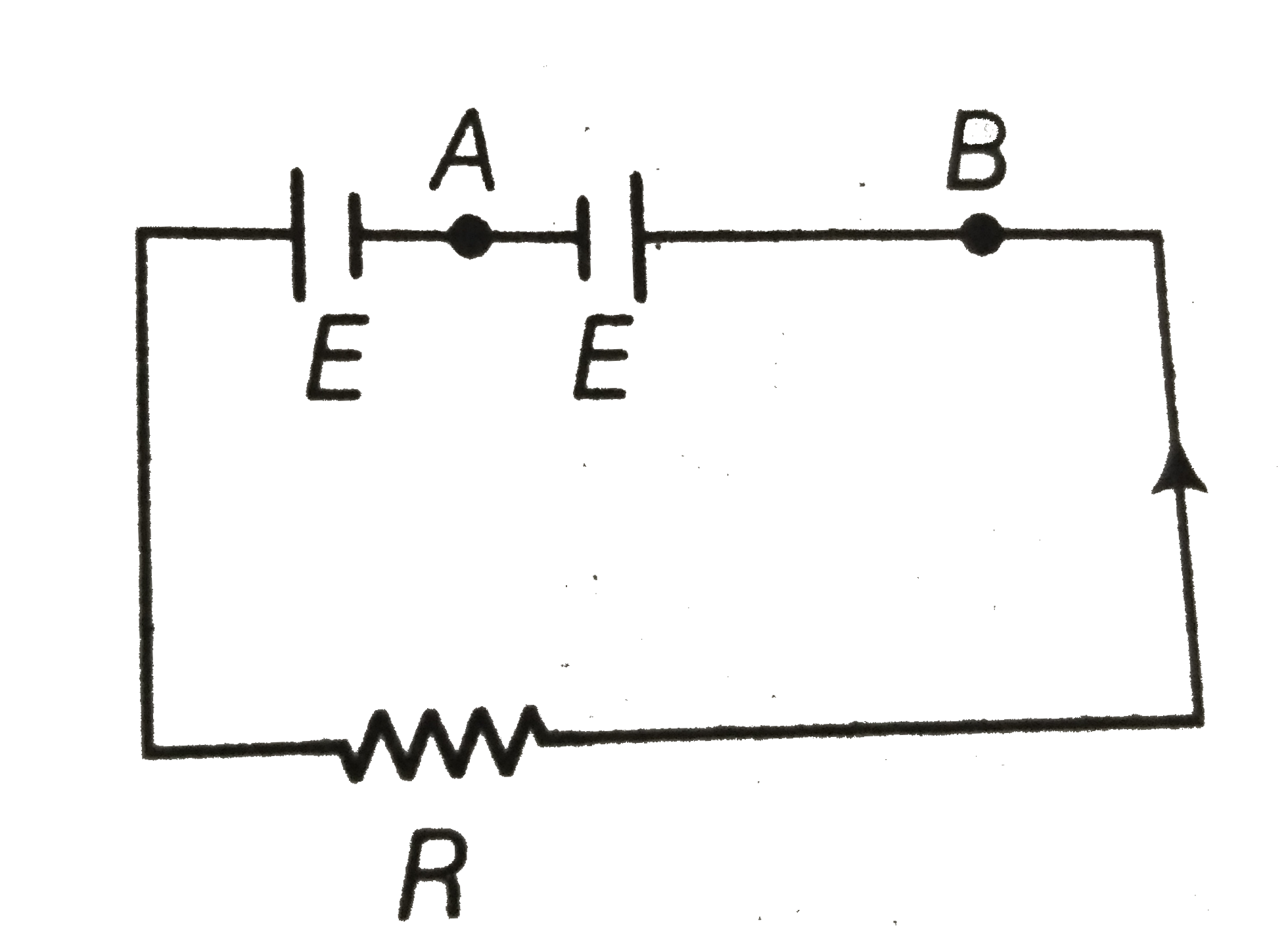
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View Solution