Two wires are held perpendicular to the plane of paper and are 5 m apart. They carry currents of 2.5 A and 5 A in same direction. Then, the magnetic field strength (B) at a point midway between the wires will be
μ04πT
μ02πT
3μ02πT
3μ04πT
The correct Answer is:b
To solve the problem of finding the magnetic field strength (B) at a point midway between two parallel wires carrying currents in the same direction, we can follow these steps:
1. Identify the Parameters:
- Distance between the wires, d=5m.
- Currents in the wires, I1=2.5A (for the first wire) and I2=5A (for the second wire).
2. Determine the Midpoint:
- The midpoint between the two wires is d2=52=2.5m from each wire.
3. Use the Formula for Magnetic Field:
- The magnetic field B due to a long straight current-carrying wire at a distance r from the wire is given by:
B=μ0I2πr
- Here, μ0 is the permeability of free space, approximately 4π×10−7T m/A.
4. Calculate Magnetic Field from Each Wire:
- For the first wire (current I1=2.5A):
B1=μ0I12πr1=μ0⋅2.52π⋅2.5=μ02π(inward direction)
- For the second wire (current I2=5A):
B2=μ0I22πr2=μ0⋅52π⋅2.5=μ0π(outward direction)
5. Determine the Direction of the Magnetic Fields:
- According to the right-hand rule:
- The magnetic field B1 from the first wire (2.5 A) is directed inward.
- The magnetic field B2 from the second wire (5 A) is directed outward.
6. Calculate the Net Magnetic Field:
- Since B1 is inward and B2 is outward, we can find the net magnetic field:
Bnet=B2−B1=μ0π−μ02π
- Simplifying this:
Bnet=2μ02π−μ02π=μ02π(outward direction)
7. Final Result:
- The magnetic field strength at the midpoint between the wires is:
B=μ02πT(outward direction)
- Distance between the wires, d=5m.
- Currents in the wires, I1=2.5A (for the first wire) and I2=5A (for the second wire).
- The midpoint between the two wires is d2=52=2.5m from each wire.
- The magnetic field B due to a long straight current-carrying wire at a distance r from the wire is given by:
B=μ0I2πr
- Here, μ0 is the permeability of free space, approximately 4π×10−7T m/A.
- For the first wire (current I1=2.5A):
B1=μ0I12πr1=μ0⋅2.52π⋅2.5=μ02π(inward direction)
B2=μ0I22πr2=μ0⋅52π⋅2.5=μ0π(outward direction)
- According to the right-hand rule:
- The magnetic field B1 from the first wire (2.5 A) is directed inward.
- The magnetic field B2 from the second wire (5 A) is directed outward.
- Since B1 is inward and B2 is outward, we can find the net magnetic field:
Bnet=B2−B1=μ0π−μ02π
- Simplifying this:
Bnet=2μ02π−μ02π=μ02π(outward direction)
- The magnetic field strength at the midpoint between the wires is:
B=μ02πT(outward direction)
Similar Questions
Two long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionTwo long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
View Solution
Knowledge Check
Two parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1
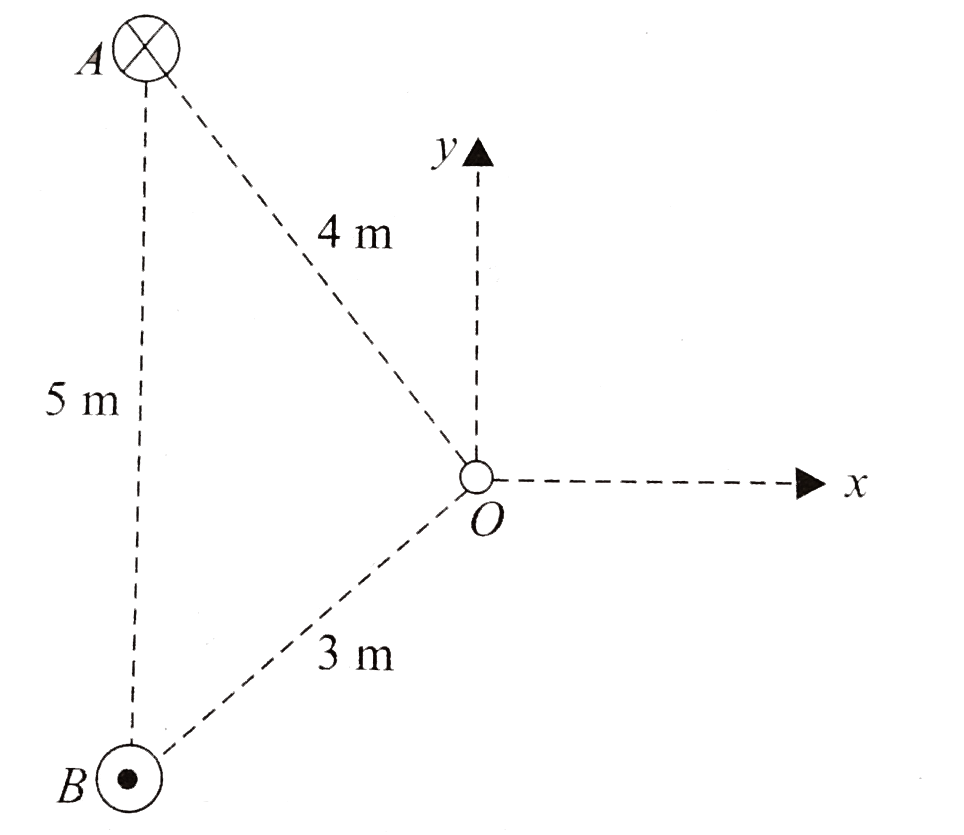
Two infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionA long straight wire in the horizontal plane carries a current of 50A in north to south direction. Give the magnitude and direction of →B at a point 2⋅5m east of the wire.
View SolutionTwo long parallel wires carry currents i1 and i2 such that i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 6×10−6T. If the direction of i2 is reversed, the field becomes 3×10−5T. The ratio i1i2 is
View SolutionTwo long parallel current carrying conductors 30 cm apart having current each of 10 A in opposite direction, then value of magentic field at a point of 10 cm between them, from any of the wire.
View SolutionThe two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
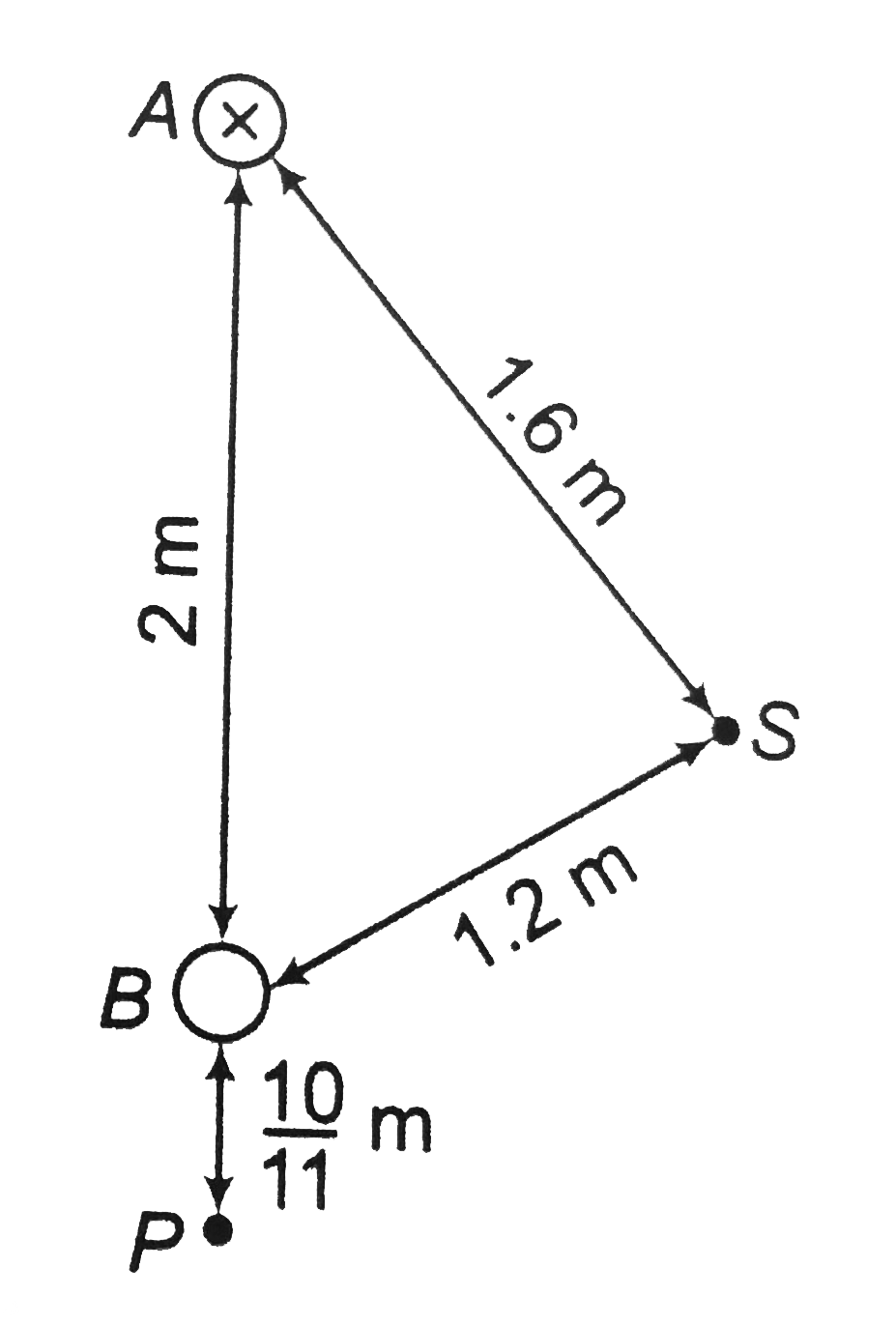
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
View Solution
