Given vectors ¯¯¯CB=¯a,¯¯¯CA=¯band¯¯¯CO=¯x where O is the centre of circle circumscribed about ΔABC, then find vector ¯x
The correct Answer is:x=b/2 or x=a/2
To solve the problem of finding the vector ¯x given the vectors ¯CB=¯a, ¯CA=¯b, and ¯CO=¯x, where O is the center of the circle circumscribed about triangle ABC, we can follow these steps:
Step 1: Write down the relationships between the vectors
From the triangle law of vector addition, we have:
¯CA+¯AB=¯CB
Substituting the given vectors:
¯b+¯AB=¯a
From this, we can express ¯AB as:
¯AB=¯a−¯b(1)
Step 2: Use the relationship involving the circumcenter
We know that the circumcenter O satisfies:
¯CO+¯OA=¯CA
Substituting the vectors:
¯x+¯OA=¯b
From this, we can express ¯OA as:
¯OA=¯b−¯x(2)
Step 3: Use another relationship involving the circumcenter
Similarly, for the vector CB:
¯CO+¯OB=¯CB
Substituting the vectors:
¯x+¯OB=¯a
From this, we can express ¯OB as:
¯OB=¯a−¯x(3)
Step 4: Equate the distances from the circumcenter to the vertices
Since O is the circumcenter, the distances from O to A, B, and C are equal:
|¯OA|=|¯OB|=|¯OC|=r
This implies:
|¯b−¯x|=|¯a−¯x|=|¯x|
Step 5: Set up the equations based on the magnitudes
From the above equalities, we can write:
1. |¯b−¯x|=r
2. |¯a−¯x|=r
3. |¯x|=r
Step 6: Solve for ¯x
From the equations, we can derive:
- From (1) and (3):
¯b−¯x=rand¯x=r
This leads to:
¯b−r=r⟹¯b=2r
- From (2) and (3):
¯a−¯x=rand¯x=r
This leads to:
¯a−r=r⟹¯a=2r
Final Result
Thus, we find:
¯x=¯a+¯b2
From the triangle law of vector addition, we have:
¯CA+¯AB=¯CB
Substituting the given vectors:
¯b+¯AB=¯a
From this, we can express ¯AB as:
¯AB=¯a−¯b(1)
We know that the circumcenter O satisfies:
¯CO+¯OA=¯CA
Substituting the vectors:
¯x+¯OA=¯b
From this, we can express ¯OA as:
¯OA=¯b−¯x(2)
Similarly, for the vector CB:
¯CO+¯OB=¯CB
Substituting the vectors:
¯x+¯OB=¯a
From this, we can express ¯OB as:
¯OB=¯a−¯x(3)
Since O is the circumcenter, the distances from O to A, B, and C are equal:
|¯OA|=|¯OB|=|¯OC|=r
This implies:
|¯b−¯x|=|¯a−¯x|=|¯x|
From the above equalities, we can write:
1. |¯b−¯x|=r
2. |¯a−¯x|=r
3. |¯x|=r
From the equations, we can derive:
- From (1) and (3):
¯b−¯x=rand¯x=r
This leads to:
¯b−r=r⟹¯b=2r
¯a−¯x=rand¯x=r
This leads to:
¯a−r=r⟹¯a=2r
Thus, we find:
¯x=¯a+¯b2
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Single Integer Answer Type Questions)
15 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
In Figure, find m ∠PQB where O is the centre of the circle
View SolutionA point O is the centre of a circle circumscribed about a triangleABC. Then →OAsin2A+→OBsin2B+→OCsin2C is equal to
View SolutionIn the given figure, O is the centre of the circle with radius 14 cm. Find the area of the shared portion

View SolutionO is the centre of a circle and an equilateral ΔABC is inscribed in it. Find the value of ∠BOC.
View SolutionIf OABC is a tetrahedron where O is the orogin anf A,B,andC are the other three vertices with position vectors, →a,→b,and→c respectively, then prove that the centre of the sphere circumscribing the tetrahedron is given by position vector a2(→b×→c)+b2(→c×→a)+c2(→a×→b)2[→a→b→c] .
View SolutionFour vectors ¯a,¯b,¯c,and¯d are lying in the same plane. The vectors ¯a and ¯b are equal in magnitude and inclined to each other at an angle of 120∘.¯¯¯C is the resultant of ¯aand¯b. Further ¯a+¯b+¯d=0. If the angle between ¯aand¯dis β and the angle between ¯aand¯cis a, find the correct relation between α and β
View SolutionA sector OABO of central angle θ is constructed in a circle with centre O and of radius 6. The radius of the circle that is circumscribed about the triangle OAB, is 6cosθ2 (b) 6secθ2 3secθ2 (d) 3(cosθ2+2)
View SolutionIn the given figure, O is the centre of a circle and ∠ADC=130∘.If ∠BAC=x∘, Find the value of x.

View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
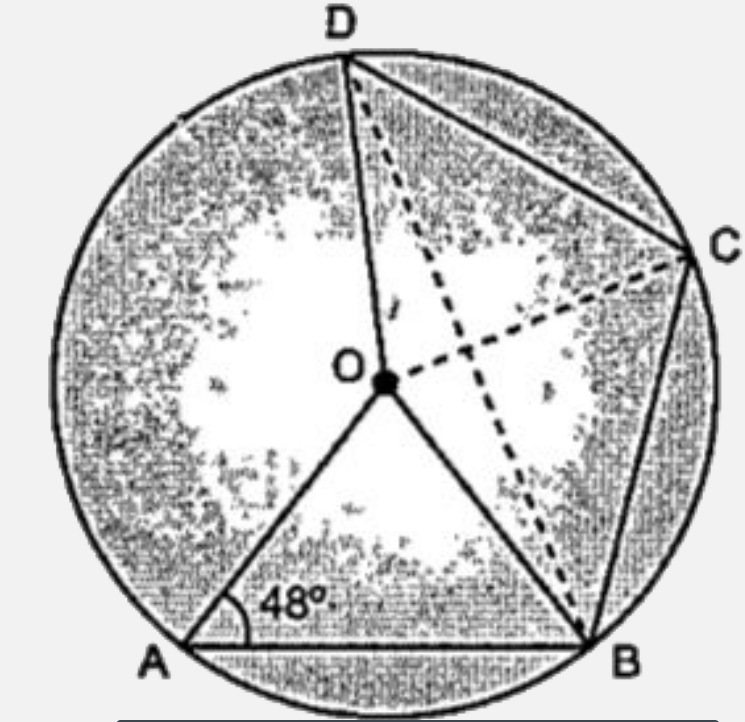
∠OBD
View SolutionAn insect crawls from A to B where B is the centre of the rectangular slant face. Find the (a) initial and final position vector of the insect and (b) displacement vector of the insect.
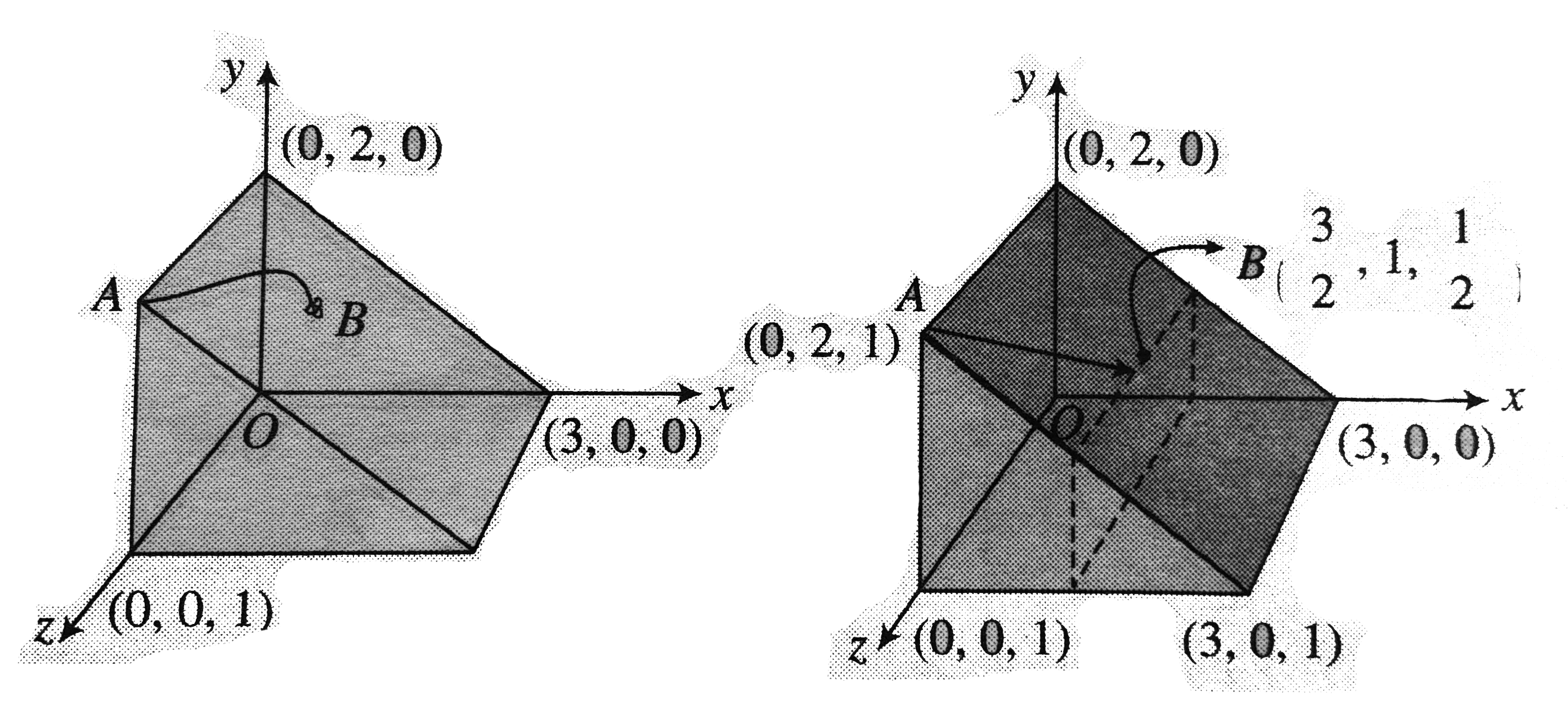 .
.
View Solution
