Given, the angles A, B and C of △ABC. Let M be the mid-point of segment AB and let D be the foot of the bisector of ∠C. Find the ratio of AreaOf△CDMAreaof△ABC
The correct Answer is:sinA−sinB2(sinA+sinB)
To find the ratio of the area of triangle CDM to the area of triangle ABC, we can follow these steps:
Step 1: Understand the Configuration
Let A, B, and C be the vertices of triangle ABC. Let M be the midpoint of segment AB and D be the foot of the bisector of angle C.
Step 2: Area of Triangle CDM
The area of triangle CDM can be expressed as:
Area of △CDM=12×DM×CT
where DM is the base and CT is the height from point C to line DM.
Step 3: Area of Triangle ABC
The area of triangle ABC can be expressed as:
Area of △ABC=12×AB×CT
where AB is the base and CT is the height from point C to line AB.
Step 4: Set Up the Ratio
Now, we can set up the ratio of the areas:
Area of △CDMArea of △ABC=12×DM×CT12×AB×CT
The CT cancels out:
=DMAB
Step 5: Find DM
Using the angle bisector theorem, we know that:
ACBC=ADDB
Let AC=b, BC=a, and AB=c. Then:
ba=ADDB
Let AD=x and DB=y. Thus:
ba=xy⟹b⋅y=a⋅x
From this, we can express AD and DB in terms of c:
AD+DB=AB⟹x+y=c
Substituting y=bax into x+y=c:
x+bax=c⟹x(1+ba)=c⟹x=c1+ba=aca+b
Thus, AD=aca+b and DB=bca+b.
Step 6: Calculate DM
Since M is the midpoint of AB:
DM=DB−MB
where MB=c2:
DM=bca+b−c2
This can be simplified further, but we can also express it in terms of c:
DM=bc−c(a+b)2a+b=2bc−c(a+b)2(a+b)=c(b−a+b2)a+b
Step 7: Final Ratio
Now substituting back into our ratio:
DMAB=c(b−a+b2)a+bc=b−a+b2a+b
This simplifies to:
2b−(a+b)2(a+b)=b−a2(a+b)
Conclusion
Thus, the final ratio of the areas is:
Area of △CDMArea of △ABC=b−a2(a+b)
Let A, B, and C be the vertices of triangle ABC. Let M be the midpoint of segment AB and D be the foot of the bisector of angle C.
The area of triangle CDM can be expressed as:
Area of △CDM=12×DM×CT
where DM is the base and CT is the height from point C to line DM.
The area of triangle ABC can be expressed as:
Area of △ABC=12×AB×CT
where AB is the base and CT is the height from point C to line AB.
Now, we can set up the ratio of the areas:
Area of △CDMArea of △ABC=12×DM×CT12×AB×CT
The CT cancels out:
=DMAB
Using the angle bisector theorem, we know that:
ACBC=ADDB
Let AC=b, BC=a, and AB=c. Then:
ba=ADDB
Let AD=x and DB=y. Thus:
ba=xy⟹b⋅y=a⋅x
From this, we can express AD and DB in terms of c:
AD+DB=AB⟹x+y=c
Substituting y=bax into x+y=c:
x+bax=c⟹x(1+ba)=c⟹x=c1+ba=aca+b
Thus, AD=aca+b and DB=bca+b.
Since M is the midpoint of AB:
DM=DB−MB
where MB=c2:
DM=bca+b−c2
This can be simplified further, but we can also express it in terms of c:
DM=bc−c(a+b)2a+b=2bc−c(a+b)2(a+b)=c(b−a+b2)a+b
Now substituting back into our ratio:
DMAB=c(b−a+b2)a+bc=b−a+b2a+b
This simplifies to:
2b−(a+b)2(a+b)=b−a2(a+b)
Thus, the final ratio of the areas is:
Area of △CDMArea of △ABC=b−a2(a+b)
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Single Integer Answer Type Questions)
15 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
Knowledge Check
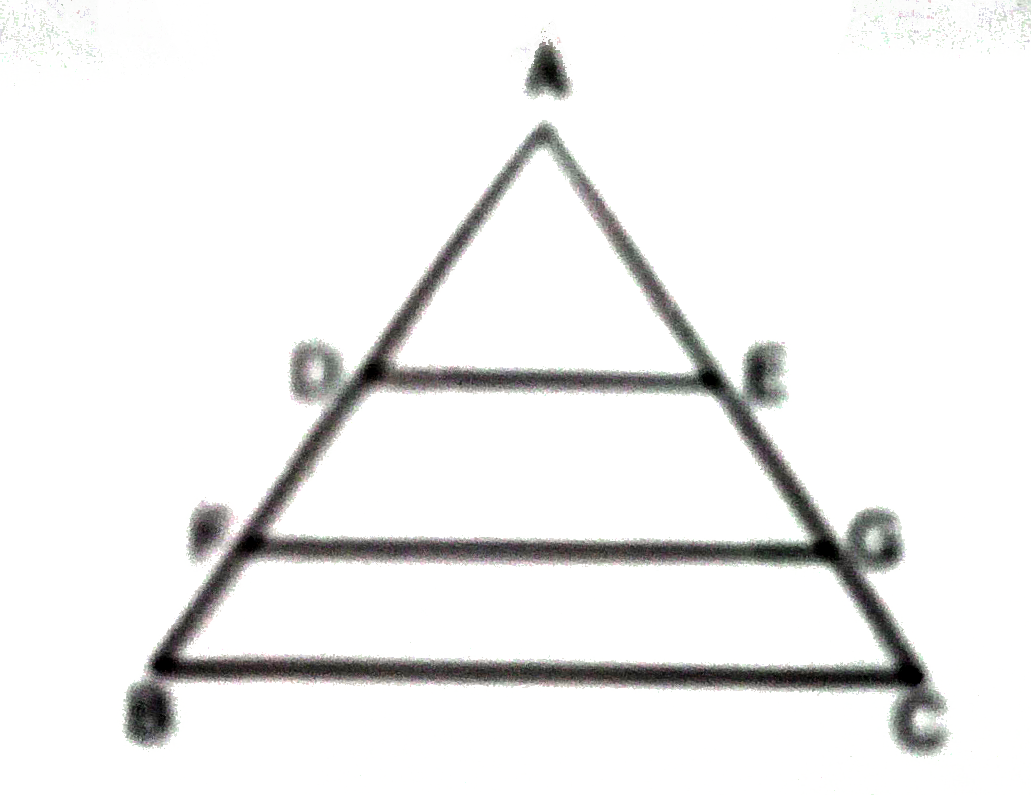In ΔABC , D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC. What is the ratio of areas of FDEG and BFGC?A5:7B3:5C2:3DData insufficient to answer
In the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
View Solution△ABC is right angled at A and AD⊥BC. If BC = 13 cm and AC= 5 cm. find the ratio of the areas of △ABCand△ADC.
View SolutionIf D, E and F are the mid-points of the sides of a △ABC , the ratio of the areas of the triangles DEF and ABC is .......
View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View SolutionIn △ABC, D is the mid point of the side AB and E is centroid of △CDA. If OE⋅CD=0, where O is the circumcentre of △ABC, using vectors prove that AB=AC.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14area of△ABC. GIVEN : A △ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
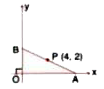
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View Solution