Given , the edges A, B and C of triangle ABC. Find cos∠BAM, where M is mid-point of BC.
The correct Answer is:sinC+sinB⋅sinA√sin2C+sin2B+2sinB⋅sinC⋅sinA
To find the cosine of angle BAM where M is the midpoint of BC in triangle ABC, we can follow these steps:
Step 1: Define the Points
Let the points A, B, and C be represented in a coordinate system. We can denote:
- A=(xA,yA)
- B=(xB,yB)
- C=(xC,yC)
Step 2: Find the Midpoint M
The coordinates of the midpoint M of segment BC can be calculated using the midpoint formula:
M=(xB+xC2,yB+yC2)
Step 3: Calculate Vectors −−→AB and −−→AM
The vector −−→AB is given by:
−−→AB=B−A=(xB−xA,yB−yA)
The vector −−→AM is given by:
−−→AM=M−A=(xB+xC2−xA,yB+yC2−yA)
Step 4: Use the Dot Product to Find cos∠BAM
The cosine of the angle BAM can be found using the dot product formula:
cos∠BAM=−−→AB⋅−−→AM|−−→AB||−−→AM|
Where:
- −−→AB⋅−−→AM=(xB−xA)(xB+xC2−xA)+(yB−yA)(yB+yC2−yA)
- |−−→AB|=√(xB−xA)2+(yB−yA)2
- |−−→AM|=√(xB+xC2−xA)2+(yB+yC2−yA)2
Step 5: Substitute and Simplify
Substituting the expressions for the dot product and magnitudes into the cosine formula will yield the value of cos∠BAM.
Conclusion
After performing the calculations and simplifications, we will arrive at the final expression for cos∠BAM.
---
Let the points A, B, and C be represented in a coordinate system. We can denote:
- A=(xA,yA)
- B=(xB,yB)
- C=(xC,yC)
The coordinates of the midpoint M of segment BC can be calculated using the midpoint formula:
M=(xB+xC2,yB+yC2)
The vector −−→AB is given by:
−−→AB=B−A=(xB−xA,yB−yA)
The vector −−→AM is given by:
−−→AM=M−A=(xB+xC2−xA,yB+yC2−yA)
The cosine of the angle BAM can be found using the dot product formula:
cos∠BAM=−−→AB⋅−−→AM|−−→AB||−−→AM|
Where:
- −−→AB⋅−−→AM=(xB−xA)(xB+xC2−xA)+(yB−yA)(yB+yC2−yA)
- |−−→AB|=√(xB−xA)2+(yB−yA)2
- |−−→AM|=√(xB+xC2−xA)2+(yB+yC2−yA)2
Substituting the expressions for the dot product and magnitudes into the cosine formula will yield the value of cos∠BAM.
After performing the calculations and simplifications, we will arrive at the final expression for cos∠BAM.
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Single Integer Answer Type Questions)
15 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
ABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14area of△ABC. GIVEN : A △ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionIn the given figure, triangle ABC is a right triangle with ∠B=90∘andD is mid-point of side BC. Prove that :
AC2=AD2+3CD2

View SolutionA (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show
that : LM=12BC.
View SolutionIn the given figure mass of string AB is 2kg. Find tension at A,B and C, where C is the mid point of string.

View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionA (-3, 4), B (3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2 : 3.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.
View SolutionD is the mid-point of side BC of △ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(△BOE)=18ar(△ABC).
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
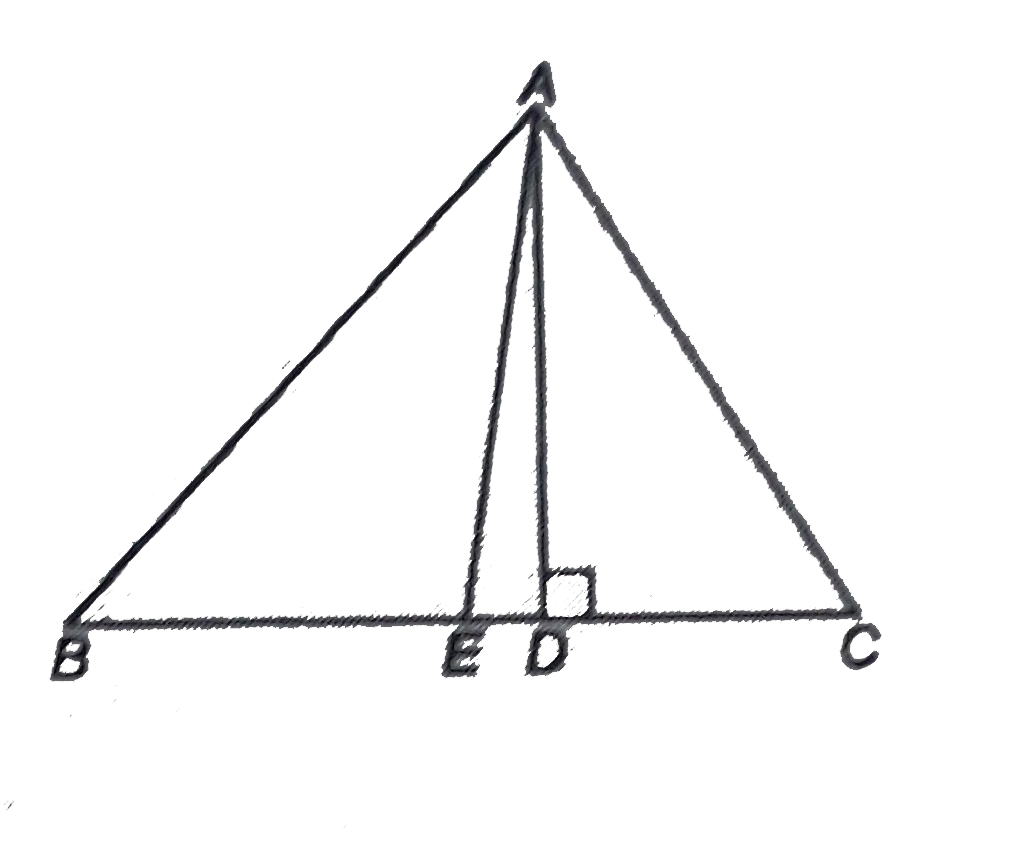
View Solution
