A particale moves under the effect of a force F=Cx from x=0 to x=x1. The work down in the process is
cx21
12cx21
x=x1
none of above
The correct Answer is:b
W=∫x10Cxdx=(1/2)Cx21
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - FRICTION22videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - MOTION IN FLUIDS25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( Laws of motion )36videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
Under the action of a force F = Cx, the position of a body changes from 0 to x. The work done is
View SolutionA particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by F=7−2x+3x2. Find the work done in the process.
View SolutionA particle moves along the X-axis x=0 to x=5 m under the influence of a force given by F=10−2x+3x2. Work done in the process is
View SolutionA particle is moving in a force field given by potential energy U=−λ(x+y+z)from point (1,1,1) to (2, 3, 4). The work done in the process is
View SolutionA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
View SolutionA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
View SolutionA particle moves under force F=5(x−2)3 .Motion of the particle is
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
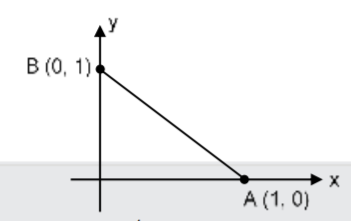 View Solution
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA particle moves under the force F(x)=(x2−6x)N, where x is in metres. For small displacements from the origin what is the force constant in the simple harmonic motion approximation ?
View Solution

